题目内容
已知sinα= ,sin(α+β)=
,sin(α+β)= ,α与β均为锐角,求cos
,α与β均为锐角,求cos .(cos
.(cos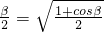 )
)
解:∵0<α< ,∴cosα=
,∴cosα=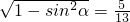 .…(2分)
.…(2分)
又∵0<α< ,0<β<
,0<β< ,
,
∴0<α+β<π.…(4分)
若0<α+β< ,∵sin(α+β)<sinα,∴α+β<α不可能.
,∵sin(α+β)<sinα,∴α+β<α不可能.
故 <α+β<π.
<α+β<π.
∴cos(α+β)=- .…(6分)
.…(6分)
∴cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα
=- •
• •
•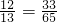 ,…(10分)
,…(10分)
∵0<β< ,
,
∴0< <
< .
.
故cos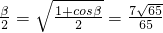 .…(13分)
.…(13分)
分析:利用同角三角函数的基本关系及角的范围,求出cosα、cos(α+β)的值,再由两角差的余弦公式可得cosβ
=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα,运算求得结果.
点评:本题主要考查两角差的余弦公式,同角三角函数的基本关系,半角公式的应用,属于中档题.
 ,∴cosα=
,∴cosα=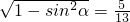 .…(2分)
.…(2分)又∵0<α<
 ,0<β<
,0<β< ,
,∴0<α+β<π.…(4分)
若0<α+β<
 ,∵sin(α+β)<sinα,∴α+β<α不可能.
,∵sin(α+β)<sinα,∴α+β<α不可能.故
 <α+β<π.
<α+β<π.∴cos(α+β)=-
 .…(6分)
.…(6分)∴cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα
=-
 •
• •
•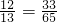 ,…(10分)
,…(10分)∵0<β<
 ,
,∴0<
 <
< .
.故cos
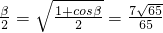 .…(13分)
.…(13分)分析:利用同角三角函数的基本关系及角的范围,求出cosα、cos(α+β)的值,再由两角差的余弦公式可得cosβ
=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα,运算求得结果.
点评:本题主要考查两角差的余弦公式,同角三角函数的基本关系,半角公式的应用,属于中档题.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
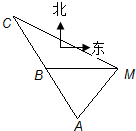 (2009•台州二模)如图,已知A、B、C是一条直路上的三点,一个人从A出发行走到B处时,望见塔M(将塔M视为与A、B、C在同一水平面上一点)在正东方向且A在东偏南α方向,继续行走1km在到达C处时,望见塔M在东偏南β方向,则塔M到直路ABC的最短距离为( )
(2009•台州二模)如图,已知A、B、C是一条直路上的三点,一个人从A出发行走到B处时,望见塔M(将塔M视为与A、B、C在同一水平面上一点)在正东方向且A在东偏南α方向,继续行走1km在到达C处时,望见塔M在东偏南β方向,则塔M到直路ABC的最短距离为( )