题目内容
设f(x)是R上的偶函数,且在[0,+∞)上递增,若f(
)=0,f(log
x)<0,那么x的取值范围是( )
| 1 |
| 2 |
| 1 |
| 4 |
分析:由题意可得:f(log
x)=f(|log
x|),结合题中的条件可得f(log
x)<f(
),即f(|log
x|)<f(
),再利用函数f(x)的单调性与对数函数的单调性即可求出x的范围.
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
解答:解:∵函数f(x)是R上的偶函数,
∴f(x)=f(-x)=f(|x|),
所以f(log
x)=f(|log
x|).
因为f(
)=0,f(log
x)<0,
所以有f(log
x)<f(
),即f(|log
x|)<f(
),
又因为函数f(x)在[0,+∞)上递增,
所以|log
x|<
,解得:
<x<2.
故选B.
∴f(x)=f(-x)=f(|x|),
所以f(log
| 1 |
| 4 |
| 1 |
| 4 |
因为f(
| 1 |
| 2 |
| 1 |
| 4 |
所以有f(log
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
又因为函数f(x)在[0,+∞)上递增,
所以|log
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
故选B.
点评:解决此类问题的关键是熟练掌握函数的奇偶性与函数的单调性及其综合应用,以及熟练掌握对数函数的单调性与特殊点,此题综合性较强属于中档题,考查学生知识的综合应用的能力.

练习册系列答案
相关题目
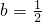 ,且k>0,问函数f(x)的图象是不是轴对称图形?如果是,求出函数f(x)图象的对称轴;如果不是,请说明理由.
,且k>0,问函数f(x)的图象是不是轴对称图形?如果是,求出函数f(x)图象的对称轴;如果不是,请说明理由. ,且k>0,问函数f(x)的图象是不是轴对称图形?如果是,求出函数f(x)图象的对称轴;如果不是,请说明理由.
,且k>0,问函数f(x)的图象是不是轴对称图形?如果是,求出函数f(x)图象的对称轴;如果不是,请说明理由.