题目内容
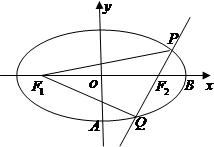
设F1,F2为椭圆 左、右焦点,过椭圆中心任作一条直线与椭圆交于P,Q两点,当四边形PF1QF2面积最大时,
左、右焦点,过椭圆中心任作一条直线与椭圆交于P,Q两点,当四边形PF1QF2面积最大时,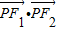 的值等于( )
的值等于( )A.0
B.1
C.2
D.4
【答案】分析:可得a,b,c的值,可得P,Q恰好是椭圆的短轴的端点时满足题意,由此可得PF1,PF2的长度和夹角,由数量积的定义可得.
解答:解:由于椭圆方程为 ,故a=2,b=
,故a=2,b= ,故c=
,故c= =1
=1
由题意当四边形PF1QF2的面积最大时,点P,Q恰好是椭圆的短轴的端点,此时PF1=PF2=a=2,
由于焦距|F1F2|=2c=2,故△PF1F2为等边三角形,故∠F1PF2=60°,
故 =2×2×cos60°=2
=2×2×cos60°=2
故选C
点评:本题考查椭圆的简单性质,判断出椭圆的四边形PF1QF2的面积最大时的情形是解决问题的关键,属中档题.
解答:解:由于椭圆方程为
 ,故a=2,b=
,故a=2,b= ,故c=
,故c= =1
=1由题意当四边形PF1QF2的面积最大时,点P,Q恰好是椭圆的短轴的端点,此时PF1=PF2=a=2,
由于焦距|F1F2|=2c=2,故△PF1F2为等边三角形,故∠F1PF2=60°,
故
 =2×2×cos60°=2
=2×2×cos60°=2故选C
点评:本题考查椭圆的简单性质,判断出椭圆的四边形PF1QF2的面积最大时的情形是解决问题的关键,属中档题.

练习册系列答案
相关题目
 已知椭圆
已知椭圆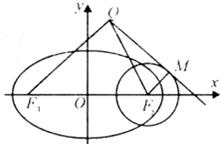 设F1,F2为椭圆C:
设F1,F2为椭圆C: