题目内容
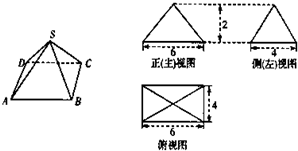 四棱锥S-ABCD的底面是矩形,顶点S在底面ABCD内的射影是矩形ABCD对角线的交点,且四棱锥及其三视图如图(AD垂直于主视图投影平面).则四棱锥的S-ABCD侧面积是
四棱锥S-ABCD的底面是矩形,顶点S在底面ABCD内的射影是矩形ABCD对角线的交点,且四棱锥及其三视图如图(AD垂直于主视图投影平面).则四棱锥的S-ABCD侧面积是分析:四棱锥是底面是长为6,宽为4的矩形,根据锥顶点在底面的射影是矩形对角线的交点,得到四个侧面是等腰三角形,根据四棱锥的高是2,底面的长和宽是6,4和勾股定理可知侧面上的高,表示出面积.
解答:解:由题意知,这是一个四棱锥,
底面是长为6,宽为4的矩形,
∵锥顶点在底面的射影是矩形对角线的交点,
∴四个侧面是等腰三角形,
∵四棱锥的高是2,底面的长和宽是6,4
根据勾股定理可知侧面上的高有
和
,
∴四个侧面的面积是2×
×6×2
+2×
×4×
=12
+4
.
故答案是:12
+4
.
底面是长为6,宽为4的矩形,
∵锥顶点在底面的射影是矩形对角线的交点,
∴四个侧面是等腰三角形,
∵四棱锥的高是2,底面的长和宽是6,4
根据勾股定理可知侧面上的高有
| 22+32 |
| 22+22 |
∴四个侧面的面积是2×
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 13 |
| 2 |
| 13 |
故答案是:12
| 2 |
| 13 |
点评:本题考查了由三视图求几何体的体积,解题的关键是判断三视图的数据所对应的几何量,利用勾股定理求侧面上的斜高.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
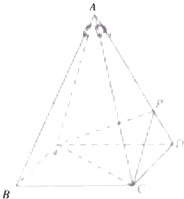 如图,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的
如图,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的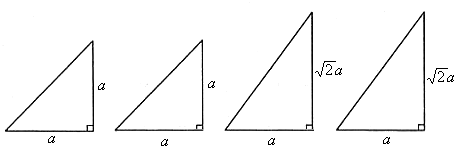
 (2012•黄浦区一模)已知四棱锥S-ABCD的底面ABCD是直角梯形,AB∥CD,BC⊥AB,侧面SAB为正三角形,AB=BC=4,CD=SD=2.如图所示.
(2012•黄浦区一模)已知四棱锥S-ABCD的底面ABCD是直角梯形,AB∥CD,BC⊥AB,侧面SAB为正三角形,AB=BC=4,CD=SD=2.如图所示. 如图已知四棱锥S-ABCD的底面是直角梯形,AB∥DC,∠DAB=90°,SA⊥底面ABCD,且SA=AD=DC=
如图已知四棱锥S-ABCD的底面是直角梯形,AB∥DC,∠DAB=90°,SA⊥底面ABCD,且SA=AD=DC=