题目内容
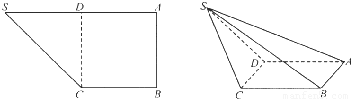
 如图已知四棱锥S-ABCD的底面是直角梯形,AB∥DC,∠DAB=90°,SA⊥底面ABCD,且SA=AD=DC=
如图已知四棱锥S-ABCD的底面是直角梯形,AB∥DC,∠DAB=90°,SA⊥底面ABCD,且SA=AD=DC=| 1 | 2 |
(1)证明:平面SAD⊥平面SCD;
(2)求AC与SB所成的角;
(3)求二面角M-AC-B的大小.
分析:(1)利用面面垂直的性质,证明CD⊥平面SAD.
(2)AC中点O,SC中点E,AB中点F,BC中点G,∠EGF是AC、SB所成的角(或补角),△EGF中,使用余弦定理求∠EGF的大小.
(3)根据三垂线定理可得,∠MOF就是二面角M-AC-B的平面角,解直角三角形求此角的大小.
(2)AC中点O,SC中点E,AB中点F,BC中点G,∠EGF是AC、SB所成的角(或补角),△EGF中,使用余弦定理求∠EGF的大小.
(3)根据三垂线定理可得,∠MOF就是二面角M-AC-B的平面角,解直角三角形求此角的大小.
解答:解:(1)由已知可得:SA⊥CD,CD⊥AD∴CD⊥平面SAD,(2分)
而CD⊆SCD,∴平面SAD⊥平面SCD(3分)
(2)设AC中点O,SC中点E,AB中点F,
BC中点G,连接OE、OF、EF、EG、FG
EG∥SB,FG∥AC,∠EGF是AC、SB所成的角(或补角)(5分)
∴OE=
SA=
,OF=
CE=
,EF=
=
又∵FG=
AC=
,EG=
SB=
∴cos∠EGF=
=
(7分)
∴AC与SB所成的角为arcos
(8分)
(3)连接MO,根据三垂线定理可得:MO⊥AC,MF⊥面ABCD,OF⊥AC
∴∠MOF就是二面角M-AC-B的平面角(10分)
tan∠MOF=
=
∴F二面角M-AC-B的大小为artan
(12分)
而CD⊆SCD,∴平面SAD⊥平面SCD(3分)
(2)设AC中点O,SC中点E,AB中点F,
BC中点G,连接OE、OF、EF、EG、FG
EG∥SB,FG∥AC,∠EGF是AC、SB所成的角(或补角)(5分)
∴OE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
(
|
| ||
| 2 |
又∵FG=
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∴cos∠EGF=
| EG2+FG2-EF2 |
| 2EG•FG |
| ||
| 5 |
∴AC与SB所成的角为arcos
| ||
| 5 |
(3)连接MO,根据三垂线定理可得:MO⊥AC,MF⊥面ABCD,OF⊥AC
∴∠MOF就是二面角M-AC-B的平面角(10分)
tan∠MOF=
| MF |
| OF |
| ||
| 2 |
∴F二面角M-AC-B的大小为artan
| ||
| 2 |
点评:本题考查证明面面垂直的方法,求线线角即二面角的方法,关键是进行等价转化.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
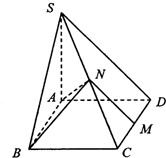 如图,已知四棱锥S-ABCD的底面ABCD是矩形,M、N分别是CD、SC的中点,SA⊥底面ABCD,SA=AD=1,AB=
如图,已知四棱锥S-ABCD的底面ABCD是矩形,M、N分别是CD、SC的中点,SA⊥底面ABCD,SA=AD=1,AB=
 (2008•湖北模拟)如图,已知四棱锥S-ABCD中,△SAD是边长为a的正三角形,平面SAD⊥平面ABCD,四边形ABCD为菱形,∠DAB=60°,P为AD的中点,Q为SB的中点.
(2008•湖北模拟)如图,已知四棱锥S-ABCD中,△SAD是边长为a的正三角形,平面SAD⊥平面ABCD,四边形ABCD为菱形,∠DAB=60°,P为AD的中点,Q为SB的中点.