题目内容
(12分)已知函数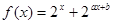 ,且
,且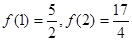
(1)求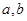 ;
;
(2)判断 的奇偶性;
的奇偶性;
(3)试判断 在
在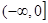 上的单调性,并证明。
上的单调性,并证明。
(1)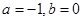 (2)偶函数(3)减函数,用定义证明即可
(2)偶函数(3)减函数,用定义证明即可
解析试题分析:(1)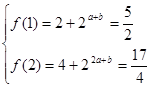 解得:
解得: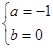 , ……2分
, ……2分
(2)由(1)得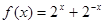 (
(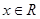 ),
),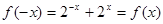 ,所以
,所以 是偶函数. ……6分
是偶函数. ……6分
(3) 在
在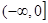 是减函数. ……8分
是减函数. ……8分
证明:设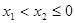 ,即
,即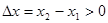
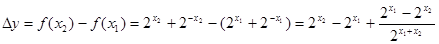
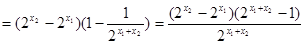 , ……10分
, ……10分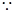
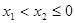
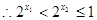 ,
,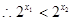 ,
,
又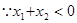
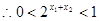 ,
,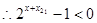 ,
,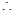
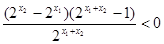 ,即
,即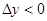 ,
,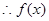 在
在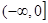 是减函数。 ……12分
是减函数。 ……12分
考点:本小题主要考查函数的解析式,奇偶性和单调性.
点评:利用定义证明函数的单调性时,要严格按照取值——作差——变形——判号——结论几个步骤进行,变形要变的彻底.

练习册系列答案
相关题目
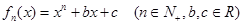
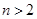 ,
,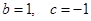 ,证明:
,证明: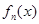 在区间
在区间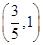 内存在唯一的零点;
内存在唯一的零点;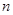 为偶数,
为偶数,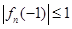 ,
,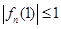 ,求
,求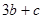 的最小值和最大值;
的最小值和最大值;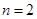 ,若对任意
,若对任意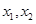
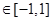 ,有
,有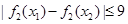 ,求
,求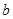 的取值范围;
的取值范围;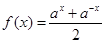 (
(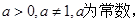 x∈R).
x∈R).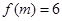 ,求
,求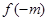 的值;
的值;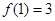 ,求
,求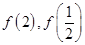 的值。
的值。
 时,求
时,求 的单调区间;
的单调区间; ,
,  恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.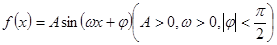 在一个周期内的部分函数图象如图所示,(I)求函数
在一个周期内的部分函数图象如图所示,(I)求函数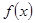 的解析式;(Ⅱ)求函数
的解析式;(Ⅱ)求函数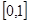 上的最大值和最小值.
上的最大值和最小值.
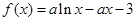 (a∈R且
(a∈R且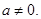 ).
). 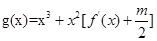 在区间(t,3)上总不是单调函数,求m的取值范围.
在区间(t,3)上总不是单调函数,求m的取值范围.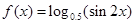
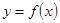 满足:对任意的实数
满足:对任意的实数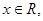 有
有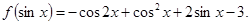
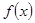 的解析式;
的解析式;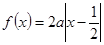 有解,求实数
有解,求实数 的取值范围.
的取值范围.