题目内容
【题目】如图1，在△ABC中， 
， 
，点D是BC的中点． （ I）求证： 
；
（ II）直线l过点D且垂直于BC，E为l上任意一点，求证： 
为常数，并求该常数；
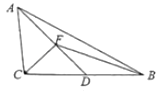
（ III）如图2，若 
，F为线段AD上的任意一点，求 
的范围．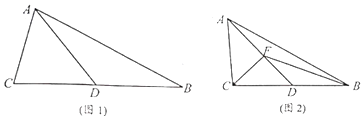
【答案】（I）证明：延长AD到A1使得AD=DA1 ， 连接CA1 ， A1B， ∵D是BC的中点，
∴四边形ACA1B是平行四边形，
∴ 
= 
+ 
，
∵ 
；
（II）证明：∵ 
= 
+ 
，
∴ （ ﹣ ）=（ + ）（ ﹣ ）= 
+ ，
∵DE⊥BC，∴ =0，
∵ = 
（ 
）= 
，
∴ ﹣ ）=
（III）解：△ABC中，| |=2，| |=1，cosA= 
， ，
∴| |= 
= 
，
同理 
+ 
=2 
，
∴ 
（ + ）= 2 =| || |，
设| |=x，则| |= ﹣x（0 
），
∴ （ + ）=2x（ ﹣x）≤2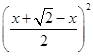 
=1，当且仅当x= 
时取等号，
∴ （ + ）∈（0，1]．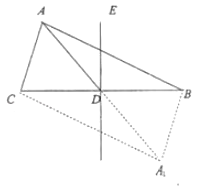
【解析】（ I）延长AD到A1使得AD=DA1 ， 连接CA1 ， A1B，证明四边形ACA1B是平行四边形，即可证明： 
；（ II）证明 
（ 
﹣ 
）=（ 
+ 
）（ ﹣ ）= 
+ ，即可得出： 
为常数，并求该常数；（III）确定 
（ 
+ 
）=2x（ 
﹣x），利用基本不等式，求 
的范围．
练习册系列答案
相关题目
