题目内容
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是 ( ).
A.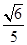 | B.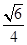 | C.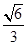 | D.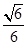 |
D
解析

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
点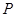 是棱长为1的正方体
是棱长为1的正方体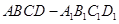 内一点,且满足
内一点,且满足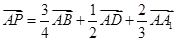 ,则点
,则点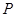 到棱
到棱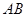 的距离为
的距离为
A.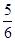 | B.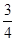 | C.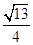 | D.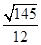 |
空间四边形ABCD的各顶点坐标分别是 ,E,F分别是AB与CD的中点,则EF的长为( )
,E,F分别是AB与CD的中点,则EF的长为( )
A. | B. | C. | D.3 |
空间直角坐标系中,点 与点
与点 的距离为
的距离为 ,则
,则 等于( )
等于( )
A. | B. | C. 或 或 | D. 或 或 |
已知正方体 中,点
中,点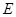 为上底面
为上底面 的中心,若
的中心,若 ,则
,则 的值是
的值是
A. | B. |
C. | D. |
已知A(1,0,0),B(0,1,0),C(0,0,1),则平面ABC的一个单位法向量是( )
A.( , , ,- ,- ) ) | B.( ,- ,- , , ) ) | C.(- , , , , ) ) | D.(- ,- ,- ,- ,- ) ) |
已知空间四边形 ,其对角线为
,其对角线为 ,
, 分别是边
分别是边 的中点,点
的中点,点 在线段
在线段 上,且使
上,且使 ,用向量
,用向量 表示向量
表示向量 是 ( )
是 ( )
A. | B. |
C. | D. |




