题目内容
如图,已知椭圆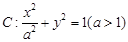 的上顶点为
的上顶点为 ,离心率为
,离心率为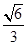 ,若不过点
,若不过点 的动直线
的动直线 与椭圆
与椭圆 相交于
相交于 、
、 两点,且
两点,且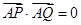 .
.
(Ⅰ)求椭圆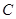 的方程;
的方程;
(Ⅱ)求证:直线 过定点,并求出该定点
过定点,并求出该定点 的坐标.
的坐标.

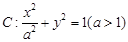 的上顶点为
的上顶点为 ,离心率为
,离心率为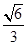 ,若不过点
,若不过点 的动直线
的动直线 与椭圆
与椭圆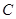 相交于
相交于 、
、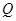 两点,且
两点,且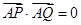 .
.(Ⅰ)求椭圆
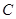 的方程;
的方程;(Ⅱ)求证:直线
 过定点,并求出该定点
过定点,并求出该定点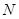 的坐标.
的坐标. 
(Ⅰ)依题意有
故椭圆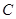 的方程为
的方程为 ……………………4分
……………………4分
(Ⅱ)(解法1)由 知
知 ,从而直线
,从而直线 与坐标轴不垂直,
与坐标轴不垂直,
由 可设直线
可设直线 的方程为
的方程为 ,
,
直线 的方程为
的方程为 .
.
将 代入椭圆
代入椭圆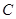 的方程
的方程 并整理得:
并整理得:  ,
,
解得 或
或 ,因此
,因此 的坐标为
的坐标为 ,
,
即 ……………………6分
……………………6分
将上式中的 换成
换成 ,得
,得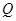
 . ………………7分
. ………………7分
直线 的方程为
的方程为
化简得直线 的方程为
的方程为 , ………………………10分
, ………………………10分
因此直线 过定点
过定点 .
.

故椭圆
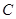 的方程为
的方程为 ……………………4分
……………………4分 (Ⅱ)(解法1)由
 知
知 ,从而直线
,从而直线 与坐标轴不垂直,
与坐标轴不垂直,由
 可设直线
可设直线 的方程为
的方程为 ,
,直线
 的方程为
的方程为 .
. 将
 代入椭圆
代入椭圆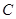 的方程
的方程 并整理得:
并整理得:  ,
,解得
 或
或 ,因此
,因此 的坐标为
的坐标为 ,
,即
 ……………………6分
……………………6分 将上式中的
 换成
换成 ,得
,得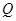
 . ………………7分
. ………………7分 直线
 的方程为
的方程为
化简得直线
 的方程为
的方程为 , ………………………10分
, ………………………10分 因此直线
 过定点
过定点 .
.略

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
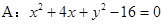 及定点
及定点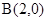 ,点Q是圆A上的动点,点G在BQ上,点P在QA上,且满足
,点Q是圆A上的动点,点G在BQ上,点P在QA上,且满足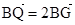 ,
,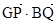 =0.
=0.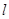 与曲线C交于M、N两点,直线
与曲线C交于M、N两点,直线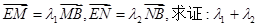 为定值。
为定值。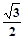 ,它与直线x+y+1=0交于P、Q两点,若OP⊥OQ,求椭圆方程。(O为原点)。
,它与直线x+y+1=0交于P、Q两点,若OP⊥OQ,求椭圆方程。(O为原点)。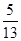 ,焦点在x轴上且长轴长为26,若曲线C2上的点到椭圆C1的两个焦点的距离的差的绝对值等于8,则曲线C2的标准方程为 _____________。
,焦点在x轴上且长轴长为26,若曲线C2上的点到椭圆C1的两个焦点的距离的差的绝对值等于8,则曲线C2的标准方程为 _____________。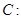
 的离心率为
的离心率为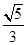 ,定点
,定点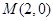 ,椭圆短轴的端点是
,椭圆短轴的端点是 ,
,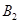 ,且
,且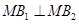 .
.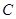 的方程;
的方程;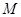 且斜率不为
且斜率不为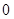 的直线交椭圆
的直线交椭圆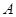 ,
,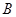 两点.试问
两点.试问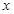 轴上是否存在定点
轴上是否存在定点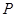 ,使
,使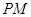 平分
平分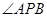 ?若存在,求出点
?若存在,求出点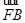 ⊥
⊥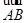 时,其离心率为
时,其离心率为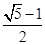 ,此类椭圆被称为“黄金椭圆”.类比“黄金椭圆”,可推算出“黄金双曲线”的离心率e等于( )
,此类椭圆被称为“黄金椭圆”.类比“黄金椭圆”,可推算出“黄金双曲线”的离心率e等于( )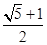
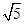 -1
-1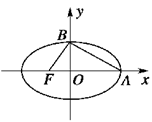
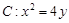 与过它的焦点F的直线
与过它的焦点F的直线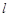 所围成封闭曲面图形的面积为
所围成封闭曲面图形的面积为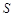 (阴影部分)。
(阴影部分)。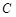 交于两点
交于两点 ,且
,且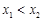 ,直线
,直线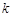 ,试用
,试用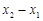 ;
;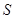 的最小值。
的最小值。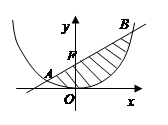
 轴上的椭圆
轴上的椭圆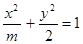 的离心率为
的离心率为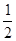 ,则m的值为( )
,则m的值为( )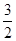
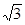
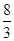
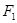 、
、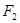 是椭圆
是椭圆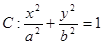 (
( >
>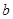 >0)的两个焦点,
>0)的两个焦点,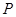 为椭圆
为椭圆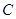 上一点,且
上一点,且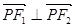 .若
.若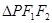 的面积为9,则
的面积为9,则