Question

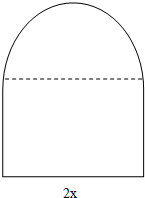用长为l的铁丝弯成下部为矩形，上部为半圆形的框架（如图），若矩形底边长为2x，求此框架围成的面积y与x的函数关系式，并写出其定义域．

Answer 1

分析：首先根据已知表示出图中的长度，然后按照已知条件列出函数表达式，通过计算求出x的取值范围即为定义域．

解答：解：∵AB=2x，
则

CD

=πx，
AD=

l-2x-πx

2

．
∴y=2x•

l-2x-πx

2

+

πx2

2

=-（

π

2

+2）x²+lx．
由

2x＞0 l-2x-πx 2

＞0，
解得0＜x＜

l

π+2

．
故答案为：{x|0＜x＜

l

π+2

}

点评：本题考查函数模型的选择与应用，通过对实际问题的分析，构造数学模型从而解决问题．需要对知识熟练的掌握并应用，属于基础题．