题目内容
 如图△ABC为正三角形,边长为2,以点A为圆心,1为半径作圆,PQ为圆A的任意一条直径.
如图△ABC为正三角形,边长为2,以点A为圆心,1为半径作圆,PQ为圆A的任意一条直径.
(1)若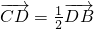 ,求
,求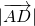 ;
;
(2)求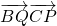 的最小值.
的最小值.
(3)判断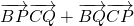 的值是否会随点P的变化而变化,请说明理由.
的值是否会随点P的变化而变化,请说明理由.
解:(1)∵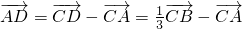 ,∴
,∴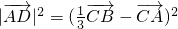 ∴=
∴=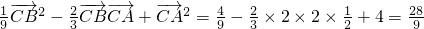 ,
,
∴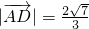
(2)设∠PAB=θ,则∠CAQ=120°-θ
∴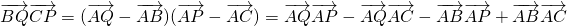 =
=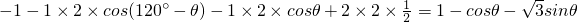 =
=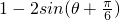
当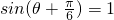 时,即
时,即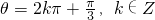 时,
时,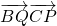 有最小值-1,
有最小值-1,
(3)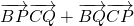 的值不随点P的变化而变化
的值不随点P的变化而变化
∵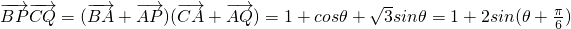
由(2)知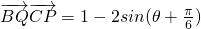 ,
,
∴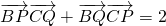 ,
,
所以∴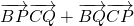 的值不随点P的变化而变化.
的值不随点P的变化而变化.
分析:(1)选定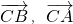 为基向量,由题设条件知,此两向量的模是2,夹角是
为基向量,由题设条件知,此两向量的模是2,夹角是 ,根据题设条件
,根据题设条件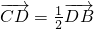 ,及向量加法用两个基向量表示出
,及向量加法用两个基向量表示出 ,再求它的模;
,再求它的模;
(2)设∠PAB=θ,则∠CAQ=120°-θ,由数量积公式及向量的三角形法则进行变形,将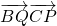 表示成∠PAB=θ的三角函数,由正弦函数的性质求出最值;
表示成∠PAB=θ的三角函数,由正弦函数的性质求出最值;
(3)由(2)将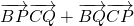 中两个向量的数量积表示成θ的三角函数,再进行运算,得出
中两个向量的数量积表示成θ的三角函数,再进行运算,得出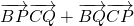 =2是一个常数由此得出结论
=2是一个常数由此得出结论
点评:本题考查向量在几何中的应用,解题的关键是掌握几何中的关系与向量的对应,本题中主要用到了线段的长度与向量的模的对应,本题考查了转化化归的思想,将求向量内积的最值的问题转化为三角函数的最值,根据所研究问题的实际情况恰当的转化研究问题的角度,是数学解题中常用的技巧,本题由有符号运算与数字运算,运算量较大,解题时要认真严谨.
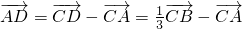 ,∴
,∴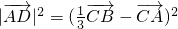 ∴=
∴=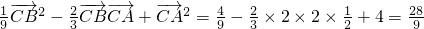 ,
,∴
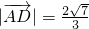
(2)设∠PAB=θ,则∠CAQ=120°-θ
∴
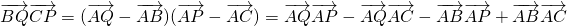 =
=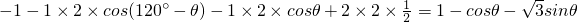 =
=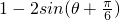
当
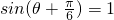 时,即
时,即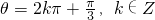 时,
时,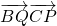 有最小值-1,
有最小值-1,(3)
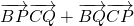 的值不随点P的变化而变化
的值不随点P的变化而变化∵
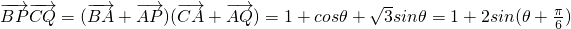
由(2)知
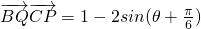 ,
,∴
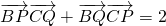 ,
,所以∴
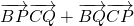 的值不随点P的变化而变化.
的值不随点P的变化而变化.分析:(1)选定
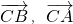 为基向量,由题设条件知,此两向量的模是2,夹角是
为基向量,由题设条件知,此两向量的模是2,夹角是 ,根据题设条件
,根据题设条件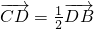 ,及向量加法用两个基向量表示出
,及向量加法用两个基向量表示出 ,再求它的模;
,再求它的模;(2)设∠PAB=θ,则∠CAQ=120°-θ,由数量积公式及向量的三角形法则进行变形,将
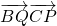 表示成∠PAB=θ的三角函数,由正弦函数的性质求出最值;
表示成∠PAB=θ的三角函数,由正弦函数的性质求出最值;(3)由(2)将
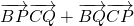 中两个向量的数量积表示成θ的三角函数,再进行运算,得出
中两个向量的数量积表示成θ的三角函数,再进行运算,得出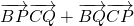 =2是一个常数由此得出结论
=2是一个常数由此得出结论点评:本题考查向量在几何中的应用,解题的关键是掌握几何中的关系与向量的对应,本题中主要用到了线段的长度与向量的模的对应,本题考查了转化化归的思想,将求向量内积的最值的问题转化为三角函数的最值,根据所研究问题的实际情况恰当的转化研究问题的角度,是数学解题中常用的技巧,本题由有符号运算与数字运算,运算量较大,解题时要认真严谨.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
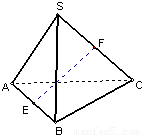
 如图,S是边长为a的正三角ABC所在平面外一点,SA=SB=SC=a,E、F是AB和SC的中点,则异面直线SA与EF所成的角为
如图,S是边长为a的正三角ABC所在平面外一点,SA=SB=SC=a,E、F是AB和SC的中点,则异面直线SA与EF所成的角为