题目内容
11．已知x的不等式x2+ax+b＜0的解集为{x|1＜x＜2}，则a2+b2=13．分析 由于不等式x2+ax+b＜0的解集为（1，2），可得1，2是方程x2+ax+b=0的实数根，利用根与系数的关系即可得出．
解答 解：∵不等式x2+ax+b＜0的解集为（1，2），
∴1，2是方程x2+ax+b=0的实数根，
∴$\left\{\begin{array}{l}{1+2=-a}\\{1×2=b}\end{array}\right.$，
解得a=-3，b=2．
∴a2+b2=9+4=13，
故答案为：13．
点评 本题考查了一元二次不等式的解法与相应的一元二次方程的实数根的关系、根与系数的关系，属于基础题．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目
2．设实数x，y满足不等式组$\left\{{\begin{array}{l}{y≥x}\\{x+y≤2}\\{x≥-1}\end{array}}\right.$．则z=3x+y的取值范围是（ ）
| A． | [-4，0] | B． | [0，4] | C． | [-2，4] | D． | [-4，4] |
19．在△ABC中，角A，B，C的对边为a，b，c，b=8，c=8$\sqrt{3}$，S△ABC=16$\sqrt{3}$，则A等于（ ）
| A． | 30° | B． | 60° | C． | 30°或150° | D． | 60°或120° |
16．在△ABC中，a，b，c分别为角A，B，C的对边，若cos2$\frac{B}{2}=\frac{a+c}{2c}$，则△ABC的形状为（ ）
| A． | 正三角形 | B． | 直角三角形 | ||
| C． | 等腰三角形 | D． | 等腰三角形或直角三角形 |
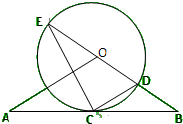（如图，直线AB经过⊙O上的点C，并且OA=OB，CA=CB，⊙O交直线OB于E，D，连接EC，CD．