题目内容
13.2016年1月2日凌晨某公司公布的元旦全天交易数据显示,天猫元旦当天全天的成交金额为315.5亿元.为了了解网购者一次性购物情况,某统计部门随机抽查了1月1日100名网购者的网购情况,得到如表数据统计表,已知网购金额在2000元以上(不含2000元)的频率为0.4.
| 网购金额(元) | 频数 | 频率 |
| (0,500] | 5 | 0.05 |
| (500,1000] | x | p |
| (1000,1500] | 15 | 0.15 |
| (1500,2000] | 25 | 0.25 |
| (2000,2500] | 30 | 0.3 |
| (2500,3000] | y | q |
| 合计 | 100 | 1.00 |
(2)对这100名网购者进一步调查显示:购物金额在2000元以上的购物者中网龄3年以上的有35人,购物金额在2000元以下(含2000元)的购物者中网龄不足3年的有20人,请填写下面的列联表,并据此判断能否在犯错误的概率不超过0.025的前提下认为网购金额超过2000元与网龄在3年以上有关?
| x | 网龄3年以上 | 网龄不足3年 | 合计 |
| 购物金额在2000元以上 | 35 | ||
| 购物金额在2000元以下 | 20 | ||
| 总计 | 100 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(3)从这100名网购者中根据购物金额分层抽出20人给予返券奖励,为进一步激发购物热情,在(2000,2500]和(2500,3000]两组所抽出的8人中再随机抽取2人各奖励1000元现金,求(2000,2500]组获得现金将的数学期望.
分析 (1)求出网购金额在2000元以上的人数,可得x,y的值,由此能求出x,y,p,q的值,并补全频率分布直方图.
(2)由数据可得列联表,利用公式,可得结论.
(3)(2000,2500]组获奖人数X为0,1,2,求出相应的概率,即可得出(2000,2500]组获得现金将的数学期望.
解答 解:(1)因为网购金额在2000元以上(不含2000元)的频率为0.4,
所以网购金额在(2500,3000]的频率为0.4-0.3=0.1,
即q=0.1,且y=100×0.1=10,
从而x=15,p=0.15,相应的频率分布直方图如图2所示.
…(4分)
(2)由题设列联表如下
| 网龄3年以上 | 网龄不足3年 | 合计 | |
| 购物金额在2000元以上 | 35 | 5 | 40 |
| 购物金额在2000元以下 | 40 | 20 | 60 |
| 合计 | 75 | 25 | 100 |
所以K2=$\frac{100×(35×20-40×5)^{2}}{75×25×40×60}$≈5.56>5.024
所以据此列联表判断,在犯错误的概率不超过0.025的前提下认为网购金额超过2000元与网龄在3年以上有关.…(8分)
(3)在(2000,2500]和(2500,3000]两组所抽出的8人中再抽取2人各奖励1000元现金,则(2000,2500]组获奖人数X为0,1,2,
且P(X=0)=$\frac{{C}_{6}^{0}{C}_{2}^{2}}{{C}_{8}^{2}}$=$\frac{1}{28}$,P(X=1)=$\frac{{C}_{6}^{1}{C}_{2}^{1}}{{C}_{8}^{2}}$=$\frac{3}{7}$,P(X=2)=$\frac{15}{28}$,
故(2000,2500]组获得现金奖的数学期望E(X)=0×$\frac{1}{28}$+1000$\frac{3}{7}$+2000×$\frac{15}{28}$=1500.…(12分)
点评 本题考查频率分布直方图,考查独立性检验的运用,考查数学期望,考查学生的计算能力,属于中档题.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
3.已知P是以F1,F2为焦点的椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上的一点,若PF1⊥PF2,且|PF1|=2|PF2|,则此椭圆的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{\sqrt{5}}{3}$ |
4.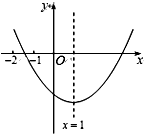 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列结论中:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列结论中:
①b2-4ac>0;
②abc>0;
③b=-2a;
④9a+3b+c<0,
正确结论的个数是( )
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列结论中:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列结论中:①b2-4ac>0;
②abc>0;
③b=-2a;
④9a+3b+c<0,
正确结论的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
1.为了得到函数y=sin2x-cos2x的图象,可以将函数y=$\sqrt{2}$cos2x的图象( )
| A. | 向左平行移动$\frac{3π}{8}$个单位 | B. | 向右平行移动$\frac{3π}{8}$个单位 | ||
| C. | 向左平行移动$\frac{3π}{4}$个单位 | D. | 向右平行移动$\frac{3π}{4}$个单位 |
8.已知|$\overrightarrow a$|=4cos$\frac{π}{8}$,|$\overrightarrow b$|=2sin$\frac{π}{8}$,$\overrightarrow a$•$\overrightarrow b$=-$\sqrt{2}$,则$\overrightarrow a$与$\overrightarrow b$的夹角为( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{3π}{4}$ | D. | $\frac{2π}{3}$ |
5.已知双曲线C:$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的渐近线方程为y=±$\frac{3}{4}$x,且其右焦点为(5,0),则双曲线C的方程为( )
| A. | $\frac{x^2}{9}-\frac{y^2}{16}=1$ | B. | $\frac{x^2}{16}-\frac{y^2}{9}=1$ | C. | $\frac{x^2}{3}-\frac{y^2}{4}=1$ | D. | $\frac{x^2}{4}-\frac{y^2}{3}=1$ |
3.命题“?x0∈(0,+∞),ln x0=x0-1”的否定是( )
| A. | ?x∈(0,+∞),ln x≠x-1 | B. | ?x∉(0,+∞),ln x=x-1 | ||
| C. | ?x0∈(0,+∞),ln x0≠x0-1 | D. | ?x0∉(0,+∞),ln x0=x0-1 |