题目内容
6.已知函数f(x)=$\left\{\begin{array}{l}-{x^2}-2x+3,x≤0\\|{2-lnx}|,x>0\end{array}\right.$,直线y=k与函数f(x)的图象相交于四个不同的点,交点的横坐标从小到大依次记为a,b,c,d,则abcd的取值范围是( )| A. | [0,e2] | B. | [0,e2) | C. | [0,e4] | D. | [0,e4) |
分析 画出y=f(x)与y=k的图象,运用韦达定理和对数的运算性质,计算即可得到所求范围.
解答  解:函数f(x)=$\left\{\begin{array}{l}-{x^2}-2x+3,x≤0\\|{2-lnx}|,x>0\end{array}\right.$的图象如下:
解:函数f(x)=$\left\{\begin{array}{l}-{x^2}-2x+3,x≤0\\|{2-lnx}|,x>0\end{array}\right.$的图象如下:
四个交点横坐标从小到大,依次记为a,b,c,d,
则a,b是x2+2x+k-3=0的两根,
由于x<0时,-x2-2x+3=4-(x+1)2≤4,
判别式为4-4(k-3)=4(4-k)>0,
即有k<4,
∴a+b=-2,ab=k-3<1,
∴ab∈[0,1),
且lnc=2-k,lnd=2+k,
∴ln(cd)=4,∴cd=e4,
∴abcd∈[0,e4),
故选:D.
点评 本题考查函数的图象,分段函数,零点与方程的根之间的关系,综合性较强.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.执行如图所示的算法流程图.若输入x=0,则输出的y的值是( )
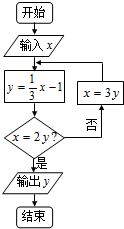

| A. | -3 | B. | -2 | C. | -1 | D. | 0 |
11.国家新闻出版广电总局电视剧管理司针对部分抗战题材电视剧存在的过度娱乐化现象,决定对各卫视电视剧黄金档已预播的抗战剧进行重审.已知全国现阶段安排预播的抗战剧共18部,其中“偶像类”、“谍战类”、“武侠类”、“爱情类”、“纪实类”等五类具体部数如下表:
(Ⅰ)若从中任意抽取2部,求所抽取的2部为同一类别抗战剧的概率;
(Ⅱ)若从中任意抽取2部,记其中“谍战类”抗战剧的部数为ξ,求随机变量ξ的分布列及数学期望.
| 类别 | 偶像类 | 谍战类 | 武侠类 | 爱情类 | 纪实类 |
| 部数 | 5 | 3 | 5 | 3 | 2 |
(Ⅱ)若从中任意抽取2部,记其中“谍战类”抗战剧的部数为ξ,求随机变量ξ的分布列及数学期望.
15.为考察某种药物预防疾病的效果,对100只某种动物进行试验,得到如下的列联表:
经计算,统计量K2的观测值k≈4.762,则在犯错误的概率不超过( )的前提下认为药物有效,已知独立性检验中统计量K2的临界值参考表为:
| 患者 | 未患者 | 合计 | |
| 服用药 | 10 | 40 | 50 |
| 没服用药 | 20 | 30 | 50 |
| 合计 | 30 | 70 | 100 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 0.005 | B. | 0.05 | C. | 0.010 | D. | 0.025 |
16.已知集合M={0,1},N={-1,0},则M∩N=( )
| A. | {-1,0,1} | B. | {-1,1} | C. | {0} | D. | φ |
