题目内容
在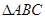 中,
中,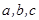 分别是角A、B、C的对边,
分别是角A、B、C的对边,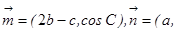
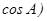 ,且
,且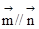 .
.
(1)求角A的大小;
(2)求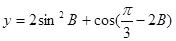 的值域.
的值域.
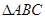 中,
中,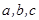 分别是角A、B、C的对边,
分别是角A、B、C的对边,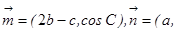
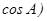 ,且
,且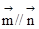 .
.(1)求角A的大小;
(2)求
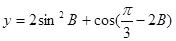 的值域.
的值域.(1) ;(2)(
;(2)( ].
].
 ;(2)(
;(2)( ].
].(1)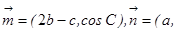
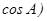 ,且
,且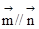 ,
,
∵(2b-c)cosA= acosC,
∴(2sinB-sinC)cosA=sinAcosC.
即2sinBcosA=sinAcosC+sinCcosA
=sin(A+C)
∵A+B+C=π, A+C=π-B,
∴sin(A+C)=sinB,
∴2sinBcosA=sinB,∵0<B<π,∴sinB≠0.
∴cosA=
∵0<A<π,∴A= .
.
(2)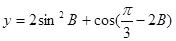
=1-cos2B+
=1-
=1+sin(2B- ),
),
由(1)知A= ,B+C=
,B+C= ,所以
,所以
0<B< ,-
,- <2B-
<2B- <
< ,-
,- <sin(2B-
<sin(2B- )≤1,
)≤1,
函数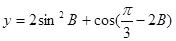 的值域是(
的值域是( ].
].
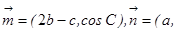
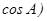 ,且
,且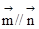 ,
,∵(2b-c)cosA= acosC,
∴(2sinB-sinC)cosA=sinAcosC.
即2sinBcosA=sinAcosC+sinCcosA
=sin(A+C)
∵A+B+C=π, A+C=π-B,
∴sin(A+C)=sinB,
∴2sinBcosA=sinB,∵0<B<π,∴sinB≠0.
∴cosA=

∵0<A<π,∴A=
 .
.(2)
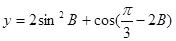
=1-cos2B+

=1-

=1+sin(2B-
 ),
),由(1)知A=
 ,B+C=
,B+C= ,所以
,所以0<B<
 ,-
,- <2B-
<2B- <
< ,-
,- <sin(2B-
<sin(2B- )≤1,
)≤1,函数
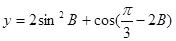 的值域是(
的值域是( ].
].
练习册系列答案
相关题目

 的值域; (3)求证:
的值域; (3)求证:

 ,函数
,函数
 的最小正周期
的最小正周期 ;
; 上个单位后,再将所得图像上所有点的横坐标伸长为原来的3倍,得到函数
上个单位后,再将所得图像上所有点的横坐标伸长为原来的3倍,得到函数 的图像,求函数
的图像,求函数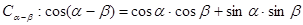 ;
;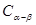 推导两角和的余弦公式
推导两角和的余弦公式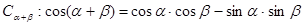 .
.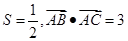 ,且
,且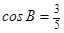 ,求
,求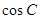 .
. 且α
且α (0,
(0, ),则cosα–sinα的值是
),则cosα–sinα的值是

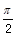 ,
,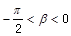 ,cos(
,cos(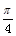 +a)=
+a)=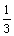 ,cos(
,cos(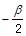 )=
)=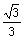 ,则cos(a+
,则cos(a+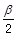 )( )
)( )

 ,
,
 ,则
,则 .
. =____________.
=____________.