题目内容
下列结论中:
(1)当x≥2时,x+
的最小值为2;
(2)当0<x≤2时,2x-2-x无最大值;
(3)当x≠0时,x+
≥2;
(4)当x>1时,lgx+
≥2.
正确的个数是( )
(1)当x≥2时,x+
| 1 |
| x |
(2)当0<x≤2时,2x-2-x无最大值;
(3)当x≠0时,x+
| 1 |
| x |
(4)当x>1时,lgx+
| 1 |
| lgx |
正确的个数是( )
分析:根据基本不等式的使用条件,判断各个选项是否正确,从而得出结论.
解答:解:(1)不正确,因为当x≥2时,x+
>2,故x+
的最小值大于2.
(2)不正确,当0<x≤2时,令t=2x,则1<t≤4,而函数 f(x)=g(t)=t-
,
再根据函数g(t)在(1,4]上是增函数,故当t=4时,函数f(x)=g(t)取得最大值为 4-
=
.
(3)不正确,例如当x=-1时,x+
=-2.
(4)正确,∵当x>1时,有lgx>0,利用基本不等式可得lgx+
≥2,当且仅当lgx=1时,即x=10时等号成立.
故选B.
| 1 |
| x |
| 1 |
| x |
(2)不正确,当0<x≤2时,令t=2x,则1<t≤4,而函数 f(x)=g(t)=t-
| 1 |
| t |
再根据函数g(t)在(1,4]上是增函数,故当t=4时,函数f(x)=g(t)取得最大值为 4-
| 1 |
| 4 |
| 15 |
| 4 |
(3)不正确,例如当x=-1时,x+
| 1 |
| x |
(4)正确,∵当x>1时,有lgx>0,利用基本不等式可得lgx+
| 1 |
| lgx |
故选B.
点评:本题主要考查基本不等式的应用,注意基本不等式的使用条件,基本不等式a+b≥2
,(当且仅当a=b时取“=”)的必须具备得使用条件:
“一正、二定、三相等”,一正(即a,b都需要是正数); 二定(求和时,积是定值;求积时,和是定值.); 三等(当且仅当a=b时,才能取等号),
属于基础题.
| ab |
“一正、二定、三相等”,一正(即a,b都需要是正数); 二定(求和时,积是定值;求积时,和是定值.); 三等(当且仅当a=b时,才能取等号),
属于基础题.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
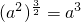 ;
; 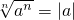 ;
; 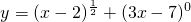 的定义域是[2,+∞);
的定义域是[2,+∞);