Question

【题目】已知点是直线与椭圆的一个公共点，分别为该椭圆的左右焦点，设取得最小值时椭圆为．

（I）求椭圆的方程；

（II）已知是椭圆上关于轴对称的两点，是椭圆上异于的任意一点，直线分别与轴交于点,试判断是否为定值，并说明理由．

Answer 1

【答案】（Ⅰ）；（Ⅱ）为定值1，理由见解析．

【解析】

试题分析：（Ⅰ）首先联立直线与椭圆方程，根据直线与椭圆有公共点利用判别式求得的取值范围，然后根据椭圆的定义即可求得椭圆的方程；（Ⅱ）首先设，，，然后根据结合点在椭圆上得到关于的表达式，由此求出定值．

试题解析：（I）将代入椭圆方程，得，

∵直线与椭圆有公共点，∴，得，

∴．………………3分

又由椭圆定义知，故当时，取得最小值，

此时椭圆的方程为．………………4分

（II）设，，，且，

∵，∴，即，

∴．………………6分

同理可得．………………7分

∴，………………9分

又，，∴，，

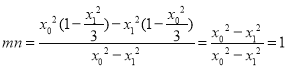∴，则为定值1．………………12分