题目内容
设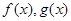 分别是定义在R上的奇函数和偶函数,当
分别是定义在R上的奇函数和偶函数,当 时,
时,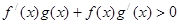 ,且
,且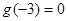 ,则
,则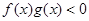 的解集是( )
的解集是( )
| A.(-3,0)∪(3,+∞) | B.(-3,0)∪(0,3) |
| C.(-∞,-3)∪(3,+∞) | D. (-∞,-3)∪(0,3) |
D
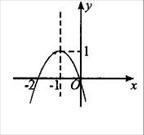
解析试题分析: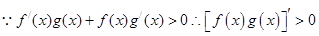 ,所以当
,所以当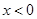 时函数
时函数 是增函数,
是增函数,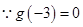
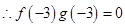
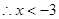 时
时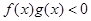 ,
,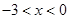 时
时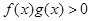 ,
,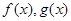 分别是定义在R上的奇函数和偶函数,所以
分别是定义在R上的奇函数和偶函数,所以 是R上的奇函数,所以当
是R上的奇函数,所以当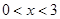 时
时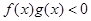 ,综上可知
,综上可知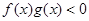 的解集为(-∞,-3)∪(0,3)
的解集为(-∞,-3)∪(0,3)
考点:利用函数性质解不等式
点评:本题首要是能够由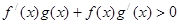 反用公式得到函数
反用公式得到函数 的单调性,进而结合图像的到
的单调性,进而结合图像的到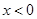 时的解集,借助于奇偶性得到R上的解集
时的解集,借助于奇偶性得到R上的解集

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知偶函数 在区间
在区间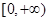 上是增函数,如果
上是增函数,如果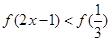 ,则
,则 的取值范围是( )
的取值范围是( )
A.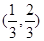 | B.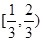 | C.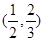 | D. |
使得函数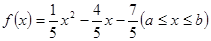 的值域为
的值域为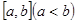 的实数对
的实数对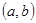
有( )对
| A.1 | B.2 | C.3 | D.无数 |
下列函数中既是偶函数,又是区间 上的减函数的是( )
上的减函数的是( )
A. | B. |
C. | D.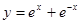 |
已知直线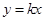 与曲线
与曲线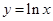 有公共交点,则
有公共交点,则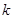 的最大值为
的最大值为
| A.1 | B. | C.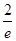 | D.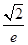 |
下列各组函数中,表示同一函数的是( )。
A.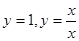 | B.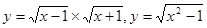 |
C.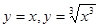 | D.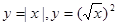 |
下列函数中,定义域为[0,∞)的函数是 ( )
A.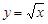 | B.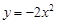 | C.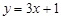 | D.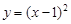 |
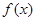 ,
,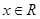 ,且
,且 ,当
,当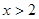 时,
时,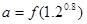 ,
,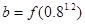 ,
,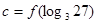 ,则
,则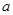 、
、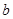 、
、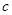 的大小顺序是( )。
的大小顺序是( )。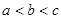
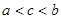
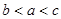
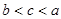
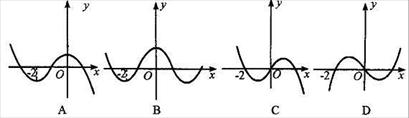
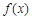 的导函数
的导函数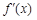 的图象如图所示,那么函数
的图象如图所示,那么函数