题目内容
已知函数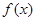 ,
,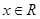 ,且
,且 ,当
,当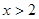 时,
时,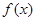 是增函数,设
是增函数,设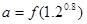 ,
,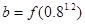 ,
,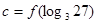 ,则
,则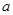 、
、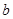 、
、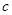 的大小顺序是( )。
的大小顺序是( )。
A.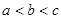 | B.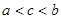 | C.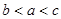 | D.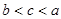 |
B
解析试题分析:因为函数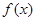 ,
,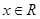 ,且
,且 ,所以,函数的图象关于直线x=2对称,又当
,所以,函数的图象关于直线x=2对称,又当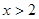 时,
时,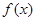 是增函数,所以函数在x<2时为减函数。而
是增函数,所以函数在x<2时为减函数。而 ,
, ,故a<c<b,选B。
,故a<c<b,选B。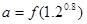
考点:本题主要考查函数的对称性,单调性,指数函数、对数函数的性质。
点评:典型题,此类题目在高考题中常常出现,难度不大,覆盖面广,对数形结合思想有较好的考查。

练习册系列答案
相关题目
函数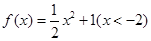 的反函数是
的反函数是
A.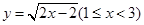 | B.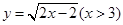 |
C.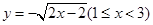 | D.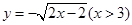 |
已知函数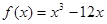 ,若
,若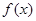 在区间
在区间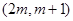 上单调递减,则实数
上单调递减,则实数 的取值范围是( )
的取值范围是( )
A.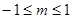 | B.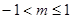 | C.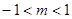 | D.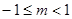 |
设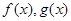 分别是定义在R上的奇函数和偶函数,当
分别是定义在R上的奇函数和偶函数,当 时,
时,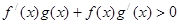 ,且
,且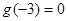 ,则
,则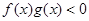 的解集是( )
的解集是( )
| A.(-3,0)∪(3,+∞) | B.(-3,0)∪(0,3) |
| C.(-∞,-3)∪(3,+∞) | D. (-∞,-3)∪(0,3) |
已知函数 的定义域为
的定义域为 ,则函数
,则函数 的定义域为
的定义域为
A. | B. | C. | D. |
函数 的定义域是( )
的定义域是( )
| A.[-1,+∞) | B.[-1,0) | C.(-1,+∞) | D.(-1,0) |
已知 ,函数
,函数 的零点个数为
的零点个数为
| A.2 | B.3 | C.4 | D.2或3或4 |
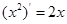 ,
, ,
,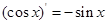 ,由归纳推理可得:若定义在
,由归纳推理可得:若定义在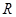 上的函数
上的函数 满足
满足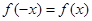 ,记
,记 为
为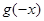 =( )
=( )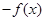 C
C 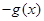
 (x>0)的图像经过矩形OABC的对角线的交点M,分别与AB、BC相交于点D、E,若四边形ODBE的面积为6,则k的值为【 】
(x>0)的图像经过矩形OABC的对角线的交点M,分别与AB、BC相交于点D、E,若四边形ODBE的面积为6,则k的值为【 】