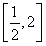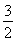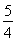题目内容

f(x)=x2+px+q，A={x|x=f(x)}，B={x|f［f(x)］=x}.

(1)求证:AB；

(2)如果A={-1,3},求B.

解析：欲证AB，只要对任意的x∈A，都有x∈B，即满足集合A的条件的元素，同时也满足集合B的条件.?

(1)证明:设x0是集合A中的任一元素，即有x0∈A,?

∵A={x|x=f(x)},∴x0=f(x0),?

即有f［f(x0)］=f(x0)=x0.?

∴x0∈B.故A?B.?

(2)解析:将-1、3代入方程x2+(p-1)x+q=0，

解得

∴方程f［f(x)］=x化为?

(x2-x-3)2-(x2-x-3)-3=x，?

即(x2-x-3)2-x2=0.?

解得x=-1,,- ,3，故B=?{-1, ,-,3}.

练习册系列答案
相关题目
对于函数y=f（x）（x∈I），y=g（x）（x∈I），若对于任意x∈I，存在x0，使得f（x）≥f（x0），g（x）≥g（x0）且f（x0）=g（x0），则称f（x），g（x）为“兄弟函数”．已知函数f(x)=x2+px+q(p，q∈R)，g(x)=
x2-x+1
x
是定义在区间x∈[
1
2
，2]上的“兄弟函数”，那么函数f（x）在区间x∈[
1
2
，2]上的最大值为（　　）
若函数f(x)=x2+px+q,f(1)=f(2)=0,则f(-1)=____________.

已知函数f(x)=x2+px+q满足f(1)=f(2)=0，则f(-1)等于(    )

A.0                     B.6                   C.3                  D.不确定

对于函数y=f(x)(x∈I),y=g(x)(x∈I),若对任意x∈I,存在x0使得f(x)≥f(x0),g(x)≥g(x0)且f(x0)=g(x0),则称f(x),g(x)为“兄弟函数”,已知f(x)=x2+px+q,g(x)=是定义在区间上的“兄弟函数”,那么函数f(x)在区间上的最大值为(　　)

(A) (B)2 (C)4 (D)

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网