题目内容
已知函数 .
.(1)设a=1时,求函数f(x)极大值和极小值;
(2)a∈R时讨论函数f(x)的单调区间.
【答案】分析:(1)a=1,f(x)= -3x+
-3x+ ln(2x+1),x>-
ln(2x+1),x>- ,可求得f′(x)=
,可求得f′(x)= ,通过将x、f(x)、f′(x)的变化情况列表可求得函数f(x)极大值和极小值;
,通过将x、f(x)、f′(x)的变化情况列表可求得函数f(x)极大值和极小值;
(2)求得f′(x)= ,通过比较2a与-
,通过比较2a与- ,2a与
,2a与 的大小,分类讨论,利用函数单调性与极值之间的关系即可求得函数f(x)的单调区间.
的大小,分类讨论,利用函数单调性与极值之间的关系即可求得函数f(x)的单调区间.
解答:解:(1)∵a=1,
∴f(x)= -3x+
-3x+ ln(2x+1),x>-
ln(2x+1),x>- ,
,
f'(x)=x-3+ =
= =
= ,…(1分)
,…(1分)
令f'(x)=0,则x= 或x=2…(2分)
或x=2…(2分)
x、f(x)、f′(x)的变化情况如下表:
…(4分)
由上表可得: ,
, …(5分)
…(5分)
(2)f'(x)=x-(1+2a)+ =
= =
=
令f'(x)=0,则x= 或x=2a…(6分)
或x=2a…(6分)
i、当2a> ,即a>
,即a> 时,
时,
所以f(x)的增区间为(- ,
, )和(2a,+∞),减区间为(
)和(2a,+∞),减区间为( ,2a)…(8分)
,2a)…(8分)
ii、当2a= ,即a=
,即a= 时,f'(x)=
时,f'(x)= ≥0在(
≥0在( ,+∞)上恒成立,
,+∞)上恒成立,
所以f(x)的增区间为( ,+∞)…(10分)
,+∞)…(10分)
iii、当- <2a<
<2a< ,即-
,即- <a<
<a< 时,
时,
所以f(x)的增区间为(- ,2a)和(
,2a)和( ,+∞),减区间为(2a,
,+∞),减区间为(2a, )…(12分)
)…(12分)
iv、当2a≤- ,即a≤-
,即a≤- 时,
时,
所以f(x)的增区间为( ,+∞),减区间为(-
,+∞),减区间为(- ,
, )…(14分)
)…(14分)
综上述:a≤- 时,f(x)的增区间为(
时,f(x)的增区间为( ,+∞),减区间为(-
,+∞),减区间为(- ,
, )-
)- <a<
<a< 时,f(x)的增区间为(-
时,f(x)的增区间为(- ,2a)和(
,2a)和( ,+∞),减区间为(2a,
,+∞),减区间为(2a, )a=
)a= 时,f(x)的增区间为(
时,f(x)的增区间为( ,+∞)a>
,+∞)a> 时,f(x)的增区间为(-
时,f(x)的增区间为(- ,
, )和(2a,+∞),减区间为(
)和(2a,+∞),减区间为( ,2a)
,2a)
说明:如果前面过程完整,最后没有综上述,可不扣分
点评:本题考查利用导数研究函数的极值与单调性,着重考查求函数极值的基本步骤,突出化归思想与分类讨论思想的考查,属于难题.
 -3x+
-3x+ ln(2x+1),x>-
ln(2x+1),x>- ,可求得f′(x)=
,可求得f′(x)= ,通过将x、f(x)、f′(x)的变化情况列表可求得函数f(x)极大值和极小值;
,通过将x、f(x)、f′(x)的变化情况列表可求得函数f(x)极大值和极小值;(2)求得f′(x)=
 ,通过比较2a与-
,通过比较2a与- ,2a与
,2a与 的大小,分类讨论,利用函数单调性与极值之间的关系即可求得函数f(x)的单调区间.
的大小,分类讨论,利用函数单调性与极值之间的关系即可求得函数f(x)的单调区间.解答:解:(1)∵a=1,
∴f(x)=
 -3x+
-3x+ ln(2x+1),x>-
ln(2x+1),x>- ,
,f'(x)=x-3+
 =
= =
= ,…(1分)
,…(1分)令f'(x)=0,则x=
 或x=2…(2分)
或x=2…(2分)x、f(x)、f′(x)的变化情况如下表:
| x | (- , , ) ) |  | ( ,2) ,2) | 2 | (2,+∞) |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | ↗ | 极大 | ↙ | 极小 | ↗ |
由上表可得:
 ,
, …(5分)
…(5分)(2)f'(x)=x-(1+2a)+
 =
= =
=
令f'(x)=0,则x=
 或x=2a…(6分)
或x=2a…(6分)i、当2a>
 ,即a>
,即a> 时,
时,| x | (- , , ) ) |  | ( ,2a) ,2a) | 2a | (2a,+∞) |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | ↗ | ↙ | ↗ |
 ,
, )和(2a,+∞),减区间为(
)和(2a,+∞),减区间为( ,2a)…(8分)
,2a)…(8分)ii、当2a=
 ,即a=
,即a= 时,f'(x)=
时,f'(x)= ≥0在(
≥0在( ,+∞)上恒成立,
,+∞)上恒成立,所以f(x)的增区间为(
 ,+∞)…(10分)
,+∞)…(10分)iii、当-
 <2a<
<2a< ,即-
,即- <a<
<a< 时,
时,| x | (- ,2a) ,2a) | 2a | (2a, ) ) |  | ( ,+∞) ,+∞) |
| f'(x) | + | 0 | - | + | |
| f(x) | ↗ | ↙ | ↗ |
 ,2a)和(
,2a)和( ,+∞),减区间为(2a,
,+∞),减区间为(2a, )…(12分)
)…(12分)iv、当2a≤-
 ,即a≤-
,即a≤- 时,
时,| x | (- , , ) ) |  | ( ,+∞) ,+∞) |
| f'(x) | - | 0 | + |
| f(x) | ↙ | ↗ |
 ,+∞),减区间为(-
,+∞),减区间为(- ,
, )…(14分)
)…(14分)综上述:a≤-
 时,f(x)的增区间为(
时,f(x)的增区间为( ,+∞),减区间为(-
,+∞),减区间为(- ,
, )-
)- <a<
<a< 时,f(x)的增区间为(-
时,f(x)的增区间为(- ,2a)和(
,2a)和( ,+∞),减区间为(2a,
,+∞),减区间为(2a, )a=
)a= 时,f(x)的增区间为(
时,f(x)的增区间为( ,+∞)a>
,+∞)a> 时,f(x)的增区间为(-
时,f(x)的增区间为(- ,
, )和(2a,+∞),减区间为(
)和(2a,+∞),减区间为( ,2a)
,2a)说明:如果前面过程完整,最后没有综上述,可不扣分
点评:本题考查利用导数研究函数的极值与单调性,着重考查求函数极值的基本步骤,突出化归思想与分类讨论思想的考查,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
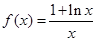 .
.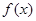 在区间
在区间 上存在极值,求实数a的取值范围;
上存在极值,求实数a的取值范围;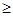 1时,不等式
1时,不等式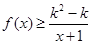 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.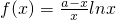 .
.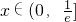 ,都有f(x)<-2,求实数a的取值范围.
,都有f(x)<-2,求实数a的取值范围. .
. ,都有f(x)<-2,求实数a的取值范围.
,都有f(x)<-2,求实数a的取值范围. .
. ,都有f(x)<-2,求实数a的取值范围.
,都有f(x)<-2,求实数a的取值范围. .
.