题目内容
如图,在四棱锥 中,底面
中,底面 为直角梯形,且
为直角梯形,且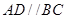 ,
, ,平面
,平面 底面
底面 ,
, 为
为 的中点,
的中点, 是棱
是棱 的中点,
的中点, .
.
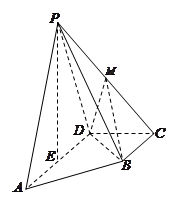

(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求三棱锥 的体积.
的体积.
 中,底面
中,底面 为直角梯形,且
为直角梯形,且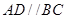 ,
, ,平面
,平面 底面
底面 ,
, 为
为 的中点,
的中点, 是棱
是棱 的中点,
的中点, .
.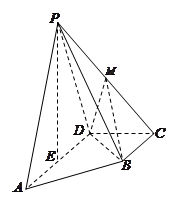

(Ⅰ)求证:
 平面
平面 ;
;(Ⅱ)求三棱锥
 的体积.
的体积.(Ⅰ)详见解析;(Ⅱ) .
.
 .
.试题分析:(Ⅰ)本小题是一个证明线面平行的题,一般借助线面平行的判定定理求解,连接
 ,因为
,因为 ,
, ,所以四边形
,所以四边形 为平行四边形,连接
为平行四边形,连接 交
交 于
于 ,连接
,连接 ,则
,则 ,则根据线面平行的判定定理可知
,则根据线面平行的判定定理可知 平面
平面 .
.(Ⅱ)由于平面
 底面
底面 ,
, ,由面面垂直的性质定理可知
,由面面垂直的性质定理可知 底面
底面 ,
,所以
 是三棱锥
是三棱锥 的高,且
的高,且 ,又因为
,又因为 可看成
可看成 和
和 差构成,由(Ⅰ)知
差构成,由(Ⅰ)知 是三棱锥
是三棱锥 的高,
的高, ,
, ,可知
,可知 ,又由于
,又由于 ,可知
,可知 .
.试题解析:连接
 ,因为
,因为 ,
, ,所以四边形
,所以四边形 为平行四边形
为平行四边形连接
 交
交 于
于 ,连接
,连接 ,则
,则 ,
,又
 平面
平面 ,
, 平面
平面 ,所以
,所以 平面
平面 .
.(2)
 ,
,由于平面
 底面
底面 ,
,
 底面
底面
所以
 是三棱锥
是三棱锥 的高,且
的高,且
由(1)知
 是三棱锥
是三棱锥 的高,
的高, ,
, ,
,所以
 ,则
,则 .
.
练习册系列答案
相关题目
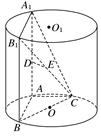
 中,AB=2BF=4,C,E分别是AB,AF的中点(如下左图).将此三角形沿CE对折,使平面AEC⊥平面BCEF(如下右图),已知D是AB的中点.
中,AB=2BF=4,C,E分别是AB,AF的中点(如下左图).将此三角形沿CE对折,使平面AEC⊥平面BCEF(如下右图),已知D是AB的中点.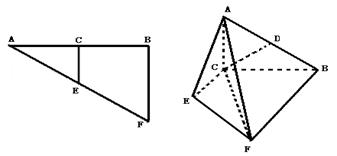
 中,
中, ,
, ,
, 是
是 上的高,沿
上的高,沿 折起,使
折起,使 .
.
 平面
平面 ;
; ,求三棱锥
,求三棱锥 的体积.
的体积.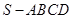 中,底面
中,底面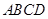 是正方形,
是正方形,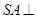 底面
底面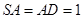 ,点
,点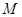 是
是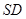 的中点,
的中点,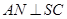 ,交
,交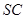 于点
于点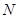 .
.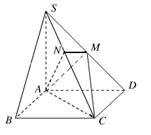
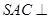 平面
平面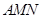 ;
;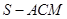 的体积.
的体积. 中,
中, 且
且 .
.
 ;
; .
. 中,AC⊥BC,AB⊥
中,AC⊥BC,AB⊥ ,
, ,D为AB的中点,且CD⊥
,D为AB的中点,且CD⊥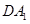 。
。
 ⊥平面ABC;
⊥平面ABC; 的体积。
的体积。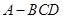 中,
中,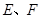 分别是
分别是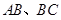 的中点,
的中点,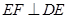 ,且
,且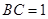 ,则正三棱锥
,则正三棱锥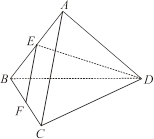
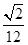
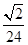
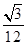
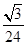
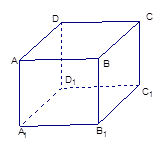
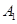 点出发沿正方体的表面到达点
点出发沿正方体的表面到达点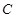 的最短路程为 .
的最短路程为 .