题目内容
已知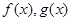 都是定义在R上的函数,
都是定义在R上的函数,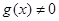 ,
,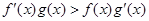 ,且
,且
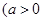 ,且
,且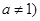 ,
,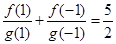 .若数列
.若数列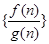 的前n项和大于62,则n的最小值为( )
的前n项和大于62,则n的最小值为( )
| A.6 | B.7 | C.8 | D.9 |
A
解析试题分析:∵ ,∴
,∴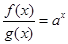 ,∵
,∵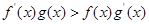 ,
,
∴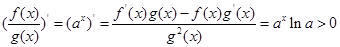 ,即
,即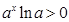 ,∴
,∴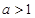 ,
,
∵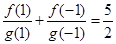 ,∴
,∴ ,∴
,∴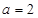 ,∴
,∴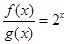 ,∴
,∴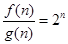 ,
,
∴数列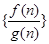 为等比数列,∴
为等比数列,∴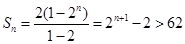 ,∴
,∴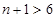 ,即
,即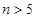 ,所以n的最小值为6,故选A.
,所以n的最小值为6,故选A.
考点:1.导数的运算;2.等比数列的前n项和公式.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
已知函数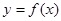 的图象关于原点对称,且当
的图象关于原点对称,且当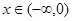 时,
时,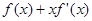
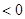 成立,(其中
成立,(其中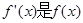 的导函数),若
的导函数),若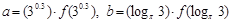 ,
,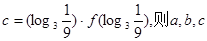 的大小关系是( )
的大小关系是( )
| A.a>b>C | B.c>b>a | C.c>a>b | D.a>c>b |
若函数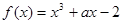 在区间
在区间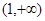 内是增函数,则实数
内是增函数,则实数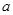 的取值范围是
的取值范围是
A.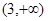 | B.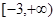 | C.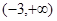 | D.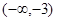 |
函数 的单调递减区间为( )
的单调递减区间为( )
A.( 1,1) 1,1) | B.(0,1] | C.[1,+∞) | D.( ∞,-1)∪(0,1] ∞,-1)∪(0,1] |
曲线y=-x3+3x2在点(1,2)处的切线方程为 ( ).
| A.y=3x-1 | B.y=-3x+5 |
| C.y=3x+5 | D.y=2x |
设底为等边三角形的直棱柱的体积为V,那么其表面积最小时,底面边
长为( )
A.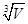 | B.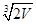 | C.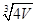 | D.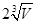 |
已知直线y=x+1与曲线y=ln(x+a)相切,则a的值为 ( ).
| A.1 | B.2 | C.-1 | D.-2 |
函数y=1+3x-x3有 ( ).
| A.极小值-1,极大值1 | B.极小值-2,极大值3 |
| C.极小值-2,极大值2 | D.极小值-1,极大值3 |
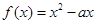 的图像在点A(l,f(1))处的切线l与直线x十3y+2=0垂直,若数列
的图像在点A(l,f(1))处的切线l与直线x十3y+2=0垂直,若数列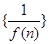 的前n项和为
的前n项和为 ,则S2013的值为 ( )
,则S2013的值为 ( )


