题目内容
已知椭圆 的左焦点为F(-
的左焦点为F(- ,0),离心率e=
,0),离心率e= ,M、N是椭圆上的动点.
,M、N是椭圆上的动点.(Ⅰ)求椭圆标准方程;
(Ⅱ)设动点P满足:
 ,直线OM与ON的斜率之积为-
,直线OM与ON的斜率之积为- ,问:是否存在定点F1,F2,使得|PF1|+|PF2|为定值?,若存在,求出F1,F2的坐标,若不存在,说明理由.
,问:是否存在定点F1,F2,使得|PF1|+|PF2|为定值?,若存在,求出F1,F2的坐标,若不存在,说明理由.(Ⅲ)若M在第一象限,且点M,N关于原点对称,点M在x轴上的射影为A,连接NA 并延长交椭圆于点B,证明:MN⊥MB.
【答案】分析:(Ⅰ)利用椭圆的左焦点为F(- ,0),离心率e=
,0),离心率e= ,建立方程组,求得几何量,从而可求椭圆的标准方程;
,建立方程组,求得几何量,从而可求椭圆的标准方程;
(Ⅱ)利用 ,确定坐标之间的关系,由直线OM与ON的斜率之积为
,确定坐标之间的关系,由直线OM与ON的斜率之积为 ,结合M、N是椭圆上的点,即可求得结论;
,结合M、N是椭圆上的点,即可求得结论;
(Ⅲ)设出坐标,证明kMN•kMB+1=0即可得到结论.
解答:(Ⅰ)解:由题设可知: ,∴a=2,c=
,∴a=2,c= …2分
…2分
∴b2=a2-c2=2…3分
∴椭圆的标准方程为: …4分
…4分
(Ⅱ)解:设P(xP,yP),M(x1,y1),N(x2,y2),由 可得:
可得: ①…5分
①…5分
由直线OM与ON的斜率之积为 可得:
可得: ,即x1x2+2y1y2=0②…6分
,即x1x2+2y1y2=0②…6分
由①②可得:xP2+2yP2=(x12+2y12)+(x22+2y22)
∵M、N是椭圆上的点,∴x12+2y12=4,x22+2y22=4
∴xP2+2yP2=8,即 …..8分
…..8分
由椭圆定义可知存在两个定点F1(-2,0),F2(2,0),使得动点P到两定点距离和为定值4 ;….9分;
;….9分;
(Ⅲ)证明:设M(x1,y1),B(x2,y2),则x1>0,y1>0,x2>0,y2>0,x1≠x2,A(x1,0),N(-x1,-y1)…..10分
由题设可知lAB斜率存在且满足kNA=kNB,∴ ….③
….③
kMN•kMB+1= +1④…12分
+1④…12分
将③代入④可得:kMN•kMB+1= +1=
+1= ⑤….13分
⑤….13分
∵点M,B在椭圆 上,∴kMN•kMB+1=
上,∴kMN•kMB+1= =0
=0
∴kMN•kMB+1=0
∴kMN•kMB=-1
∴MN⊥MB…14分.
点评:本题考查椭圆的标准方程,考查轨迹方程的求法,考查学生的计算能力,考查分析解决问题的能力.
 ,0),离心率e=
,0),离心率e= ,建立方程组,求得几何量,从而可求椭圆的标准方程;
,建立方程组,求得几何量,从而可求椭圆的标准方程;(Ⅱ)利用
 ,确定坐标之间的关系,由直线OM与ON的斜率之积为
,确定坐标之间的关系,由直线OM与ON的斜率之积为 ,结合M、N是椭圆上的点,即可求得结论;
,结合M、N是椭圆上的点,即可求得结论;(Ⅲ)设出坐标,证明kMN•kMB+1=0即可得到结论.
解答:(Ⅰ)解:由题设可知:
 ,∴a=2,c=
,∴a=2,c= …2分
…2分∴b2=a2-c2=2…3分
∴椭圆的标准方程为:
 …4分
…4分(Ⅱ)解:设P(xP,yP),M(x1,y1),N(x2,y2),由
 可得:
可得: ①…5分
①…5分由直线OM与ON的斜率之积为
 可得:
可得: ,即x1x2+2y1y2=0②…6分
,即x1x2+2y1y2=0②…6分由①②可得:xP2+2yP2=(x12+2y12)+(x22+2y22)
∵M、N是椭圆上的点,∴x12+2y12=4,x22+2y22=4
∴xP2+2yP2=8,即
 …..8分
…..8分由椭圆定义可知存在两个定点F1(-2,0),F2(2,0),使得动点P到两定点距离和为定值4
 ;….9分;
;….9分;(Ⅲ)证明:设M(x1,y1),B(x2,y2),则x1>0,y1>0,x2>0,y2>0,x1≠x2,A(x1,0),N(-x1,-y1)…..10分
由题设可知lAB斜率存在且满足kNA=kNB,∴
 ….③
….③kMN•kMB+1=
 +1④…12分
+1④…12分将③代入④可得:kMN•kMB+1=
 +1=
+1= ⑤….13分
⑤….13分∵点M,B在椭圆
 上,∴kMN•kMB+1=
上,∴kMN•kMB+1= =0
=0∴kMN•kMB+1=0
∴kMN•kMB=-1
∴MN⊥MB…14分.
点评:本题考查椭圆的标准方程,考查轨迹方程的求法,考查学生的计算能力,考查分析解决问题的能力.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 的左焦点为F,O为坐标原点.
的左焦点为F,O为坐标原点.
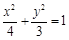 的左焦点为F,过点F的直线交椭圆于A、B两点,线段AB的中点为G,AB的中垂线与x轴和y轴分别交于D、E两点.
的左焦点为F,过点F的直线交椭圆于A、B两点,线段AB的中点为G,AB的中垂线与x轴和y轴分别交于D、E两点.
 ,求直线AB的斜率;
,求直线AB的斜率; 的左焦点为F,左右顶点分别为A、C,
的左焦点为F,左右顶点分别为A、C, ,其中圆心P的坐标为
,其中圆心P的坐标为 .
. ,求
,求 上,求椭圆的方程.
上,求椭圆的方程. 的左焦点为F,右顶点为A,点B在椭圆上,且
的左焦点为F,右顶点为A,点B在椭圆上,且 轴,直线AB交
轴,直线AB交 轴于点P。若
轴于点P。若 ,则椭圆的离心率为
,则椭圆的离心率为