题目内容
9.已知函数f(x)=$\sqrt{3}$sinωxcosωx-cos2ωx-$\frac{1}{2}$(ω>0,x∈R)的图象上相邻两个最高点的距离为π,将函数f(x)的图象向左平移$\frac{π}{6}$个单位后得函数g(x),设△ABC三个内角A、B、C的对边分别为a、b、c.(1)若c=$\sqrt{7}$,f(C)=0,sinB=3sinA,求a、b的值;
(2)若g(B)+g(-B)=-$\frac{3}{2}$,B∈(0,$\frac{π}{2}$),且向量$\overrightarrow{m}$=(cosA,cosB),$\overrightarrow{n}$=(1,sinA-cosAtanB),求$\overrightarrow{m}$•$\overrightarrow{n}$的取值范围.
分析 (1)由条件利用三角函数的恒等变换求得f(x)的解析式,由f(C)=0求得C的值,由sinB=3sinA利用正弦定理可得b=3a,再由条件利用余弦定理求得a,b的值.
(2)函数y=Asin(ωx+φ)的图象变换规律求得g(x)的解析式.再根据g(B)+g(-B)=0,求得cos2B的值,可得B的值.利用向量的数量积及A的范围即可得解.
解答 解:(1)函数f(x)=$\sqrt{3}$sinωxcosωx-cos2ωx-$\frac{1}{2}$=$\frac{\sqrt{3}}{2}$sin2ωx-$\frac{1}{2}$cos2ωx-1=sin(2ωx-$\frac{π}{6}$)-1.
∵图象上相邻两个最高点的距离为π,可得最小正周期T=$\frac{2π}{2ω}$=π,求得ω=1,f(x)=sin(2x-$\frac{π}{6}$)-1.
将函数f(x)=sin(2x-$\frac{π}{6}$)-1的图象向左平移$\frac{π}{6}$个单位后得函数g(x)=sin[2(x+$\frac{π}{6}$)-$\frac{π}{6}$]-1=sin(2x+$\frac{π}{6}$)-1.
∵c=$\sqrt{7}$,f(C)=sin(2C-$\frac{π}{6}$)-1=0,∴sin(2C-$\frac{π}{6}$)=1,∴2C-$\frac{π}{6}$=$\frac{π}{2}$,∴C=$\frac{π}{3}$.
∵sinB=3sinA,∴b=3a,由余弦定理可得c2=7=a2+(3a)2-2a•3a•cos$\frac{π}{3}$,
求得a=1,∴b=3.
(2)由于g(B)+g(-B)=sin(2B+$\frac{π}{6}$)-1+sin(-2B+$\frac{π}{6}$)-1=sin2Bcos$\frac{π}{6}$+cos2Bsin$\frac{π}{6}$-sin2Bcos$\frac{π}{6}$+cos2Bsin$\frac{π}{6}$-2=-$\frac{3}{2}$,
求得cos2B=$\frac{1}{2}$,结合B∈(0,$\frac{π}{2}$),可得2B=$\frac{π}{3}$,B=$\frac{π}{6}$.
∴$\overrightarrow{m}$•$\overrightarrow{n}$=cosA+cosB(sinA-cosAtanB)=cosA+$\frac{\sqrt{3}}{2}$(sinA-$\frac{\sqrt{3}}{3}$cosA)=$\frac{1}{2}$cosA+$\frac{\sqrt{3}}{2}$sinA=sin(A+$\frac{π}{6}$),
∵0$<A<\frac{5π}{6}$,$\frac{π}{6}$<A+$\frac{π}{6}$<π,
∴0<sin(A+$\frac{π}{6}$)<1,故$\overrightarrow{m}$•$\overrightarrow{n}$的取值范围为:(0,1).
点评 本题主要考查三角函数的恒等变换,函数y=Asin(ωx+φ)的图象变换规律,两角和差的正弦公式,正弦定理和余弦定理,正弦函数的图象,属于中档题.

 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案| A. | $\frac{π}{2}$ | B. | π | C. | 4π | D. | 8π |
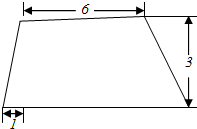 已知一圆台的轴截面如图所示,则它的内接四棱台体积的最大值为( )
已知一圆台的轴截面如图所示,则它的内接四棱台体积的最大值为( )| A. | 37 | B. | 74 | C. | 111 | D. | 222 |
 如图所示,在△ABC中,已知D为AB的中点,E为AC的中点,试判断$\overrightarrow{DE}$与$\overrightarrow{BC}$是否共线.
如图所示,在△ABC中,已知D为AB的中点,E为AC的中点,试判断$\overrightarrow{DE}$与$\overrightarrow{BC}$是否共线.