题目内容
7.已知a,b,c∈R,若|acos2x+bsinx+c|≤1对x∈R成立,则|asinx+b|的最大值为2.分析 由题意,设t=sinx,t∈[-1,1],则|at2-bt-a-c|≤1恒成立,不妨设t=1,则|b+c|≤1;t=0,则|a+c|≤1,t=-1,则|b-c|≤1,再分类讨论,利用绝对值不等式,即可得出结论.
解答 解:由题意,设t=sinx,t∈[-1,1],则|at2-bt-a-c|≤1恒成立,
不妨设t=1,则|b+c|≤1;t=0,则|a+c|≤1,t=-1,则|b-c|≤1
若a,b同号,则|asinx+b|的最大值为|a+b|=|a+c+b-c|≤|a+c|+|b-c|≤2;
若a,b异号,则|asinx+b|的最大值为|a-b|=|a+c-b-c|≤|a+c|+|b+c|≤2;
综上所述,|asinx+b|的最大值为2,
故答案为2.
点评 本题考查绝对值不等式,考查分类讨论的数学思想,属于中档题.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
2.若直线y=x+b与圆x2+y2=1有公共点,则实数b的取值范围是( )
| A. | [-1,1] | B. | [0,1] | C. | [0,$\sqrt{2}$] | D. | [-$\sqrt{2}$,$\sqrt{2}$] |
12.已知F1、F2是椭圆和双曲线的公共焦点,P是他们的一个公共点,且∠F1PF2=$\frac{π}{3}$,则椭圆和双曲线的离心率之积的最小值为( )
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
16. 某商场对一个月内每天的顾客人数进行统计,得到如图所示的样本茎叶图,则该样本的中位数和众数分别是( )
某商场对一个月内每天的顾客人数进行统计,得到如图所示的样本茎叶图,则该样本的中位数和众数分别是( )
 某商场对一个月内每天的顾客人数进行统计,得到如图所示的样本茎叶图,则该样本的中位数和众数分别是( )
某商场对一个月内每天的顾客人数进行统计,得到如图所示的样本茎叶图,则该样本的中位数和众数分别是( )| A. | 46,45 | B. | 45,46 | C. | 45,45 | D. | 47,45 |
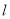 的参数方程式
的参数方程式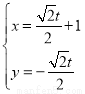 (
(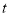 是参数).以坐标原点为极点,
是参数).以坐标原点为极点,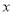 轴的正半轴为极轴,且取相同的长度单位建立极坐标系,圆
轴的正半轴为极轴,且取相同的长度单位建立极坐标系,圆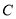 的极坐标方程为
的极坐标方程为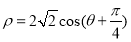 .
.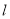 的普通方程与圆
的普通方程与圆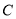 的直角坐标方程;
的直角坐标方程;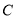 与直线
与直线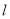 交于
交于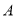 、
、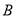 两点,若
两点,若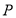 点的直角坐标为
点的直角坐标为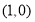 ,求
,求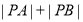 的值.
的值.