题目内容
若直线![]() 与椭圆
与椭圆![]() 恒有公共点,求实数
恒有公共点,求实数![]() 的取值范围
的取值范围
解法一:
由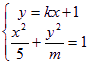 可得
可得![]() ,
,![]() 即
即![]()
![]()
解法二:直线恒过一定点![]()
当![]() 时,椭圆焦点在
时,椭圆焦点在![]() 轴上,短半轴长
轴上,短半轴长![]() ,要使直线与椭圆恒有交点则
,要使直线与椭圆恒有交点则![]() 即
即![]()
当![]() 时,椭圆焦点在
时,椭圆焦点在![]() 轴上,长半轴长
轴上,长半轴长![]() 可保证直线与椭圆恒有交点即
可保证直线与椭圆恒有交点即![]()
综述:![]()
解法三:直线恒过一定点![]()
要使直线与椭圆恒有交点,即要保证定点![]() 在椭圆内部
在椭圆内部![]()
即![]()
![]()
解析:
由直线方程与椭圆方程联立的方程组解的情况直接导致两曲线的交点状况,而方程解的情况由判别式来决定,直线与椭圆有相交、相切、相离三种关系,直线方程与椭圆方程联立,消去![]() 或
或![]() 得到关于
得到关于![]() 或
或![]() 的一元二次方程,则(1)直线与椭圆相交
的一元二次方程,则(1)直线与椭圆相交![]() (2)直线与椭圆相切
(2)直线与椭圆相切![]() (3)直线与椭圆相离
(3)直线与椭圆相离![]() ,所以判定直线与椭圆的位置关系,方程及其判别式是最基本的工具。或者可首先判断直线是否过定点,并且初定定点在椭圆内、外还是干脆就在椭圆上,然后借助曲线特征判断
,所以判定直线与椭圆的位置关系,方程及其判别式是最基本的工具。或者可首先判断直线是否过定点,并且初定定点在椭圆内、外还是干脆就在椭圆上,然后借助曲线特征判断

练习册系列答案
相关题目
 :方程
:方程 表示双曲线,
表示双曲线, :过点
:过点 的直线与椭圆
的直线与椭圆 恒有公共点,若
恒有公共点,若 为真命题,求
为真命题,求 的取值范围.
的取值范围.
 表示双曲线,q:过点M(2,1)的直线与椭圆
表示双曲线,q:过点M(2,1)的直线与椭圆 恒有公共点,若p∧q为真命题,求k的取值范围.
恒有公共点,若p∧q为真命题,求k的取值范围. 表示双曲线,q:过点M(2,1)的直线与椭圆
表示双曲线,q:过点M(2,1)的直线与椭圆 恒有公共点,若p∧q为真命题,求k的取值范围.
恒有公共点,若p∧q为真命题,求k的取值范围. 表示双曲线,q:过点M(2,1)的直线与椭圆
表示双曲线,q:过点M(2,1)的直线与椭圆 恒有公共点,若p∧q为真命题,求k的取值范围.
恒有公共点,若p∧q为真命题,求k的取值范围.