题目内容
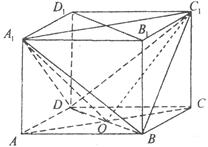
(文科)(本小题满分12分)长方体 中,
中, ,
,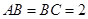 ,
,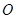 是底面对角线的交点.
是底面对角线的交点.

(Ⅰ) 求证: 平面
平面 ;
;
(Ⅱ) 求证: 平面
平面 ;
;
(Ⅲ) 求三棱锥 的体积。
的体积。
【答案】
(Ⅰ)由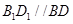 ,
,
且 在平面
在平面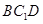 外.得
外.得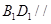 平面;
平面;
(Ⅱ)连结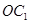 得到
得到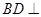 平面
平面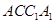 ;
;
又∵ 在
在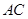 上,可得
上,可得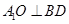 ;
;
计算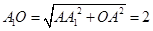 ;
;
同理: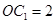 ∵
∵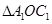 中,
中,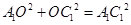
推出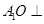 平面
平面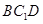 。
。
(Ⅲ)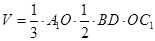
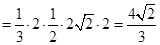 。
。
【解析】
试题分析:(Ⅰ) 证明:依题意: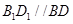 ,
,
且 在平面
在平面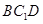 外.…2分
外.…2分
∴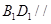 平面
平面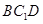 3分
3分
(Ⅱ) 证明:连结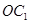 ∵
∵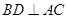
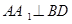
∴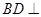 平面
平面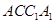 4分
4分
又∵ 在
在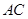 上,∴
上,∴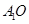 在平面
在平面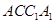 上
上
∴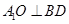 5分
5分
∵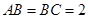 ∴
∴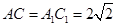
∴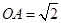 ∴
∴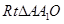 中,
中,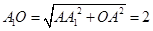 6分
6分
同理: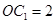 ∵
∵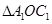 中,
中,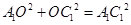
∴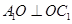 7分,∴
7分,∴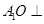 平面
平面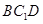 8分
8分
(Ⅲ)解:∵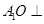 平面
平面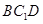 ∴所求体积
∴所求体积
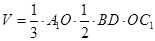
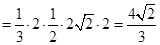 12分
12分
考点:本题主要考查立体几何中的平行关系、垂直关系,几何体体积的计算。
点评:典型题,立体几何题,是高考必考内容,往往涉及垂直关系、平行关系、角、距离、体积的计算。在计算问题中,有“几何法”和“向量法”。利用几何法,要遵循“一作、二证、三计算”的步骤。利用向量可简化证明过程。本题难度不大。

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
(文科)(本小题满分12分)某高校从参加今年自主招生考试的学生中随机抽取容量为50的学生成绩样本,得频率分布表如下:
|
组号 |
分组 |
频数 |
频率 |
|
第一组 |
[230,235) |
8 |
0.16 |
|
第二组 |
[235,240) |
① |
0.24 |
|
第三组 |
[240,245) |
15 |
② |
|
第四组 |
[245,250) |
10 |
0.20 |
|
第五组 |
[250,255] |
5 |
0.10 |
|
合 计 |
50 |
1.00 |
(1)写出表中①②位置的数据;
(2)为了选拔出更优秀的学生,高校决定在第三、四、五组中用分层抽样法抽取6名学生进行第二轮考核,分别求第三、四、五各组参加考核人数;
(3)在(2)的前提下,高校决定在这6名学生中录取2名学生,求2人中至少有1名是第四组的概率.

 过点
过点 ,离心率为
,离心率为 ,圆
,圆 的圆心为坐标原点,直径为椭圆的短轴,圆
的圆心为坐标原点,直径为椭圆的短轴,圆 的方程为
的方程为 .过圆
.过圆 作圆
作圆 ,切点为
,切点为 .
. 与圆
与圆 ,当弦
,当弦 最大时,求直线
最大时,求直线 的最值.
的最值.