题目内容
等差数列{an}中有两项am和ak满足 (其中m,k∈N*,且m≠k),则该数列前mk项之和是( )
(其中m,k∈N*,且m≠k),则该数列前mk项之和是( )A.

B.

C.

D.

【答案】分析:利用等差数列的性质先求出公差d=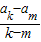 =
=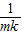 ,再根据a1+(m-1)d=am,求出a1,进而求出amk,然后用求和公式求解即可.
,再根据a1+(m-1)d=am,求出a1,进而求出amk,然后用求和公式求解即可.
解答:解:设等差数列{an}的首项为a1,公差为d,
由等差数列的性质以及已知条件得d=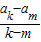 =
=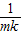 ,
,
∵a1+(m-1)d=am,
∴a1=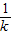 -(m-1)
-(m-1)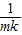 =
=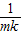 ,
,
∴amk=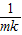 +(mk-1)
+(mk-1)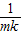 =1,
=1,
∴smk=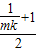 ×mk=
×mk=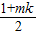 ,
,
故选C.
点评:本题考查了等差数列的性质、通项公式、前n项和公式,熟练应用公式是解题的关键,同时还考查了学生的运算能力.
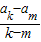 =
=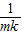 ,再根据a1+(m-1)d=am,求出a1,进而求出amk,然后用求和公式求解即可.
,再根据a1+(m-1)d=am,求出a1,进而求出amk,然后用求和公式求解即可.解答:解:设等差数列{an}的首项为a1,公差为d,
由等差数列的性质以及已知条件得d=
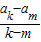 =
=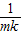 ,
,∵a1+(m-1)d=am,
∴a1=
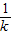 -(m-1)
-(m-1)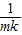 =
=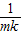 ,
,∴amk=
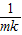 +(mk-1)
+(mk-1)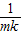 =1,
=1,∴smk=
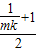 ×mk=
×mk=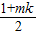 ,
,故选C.
点评:本题考查了等差数列的性质、通项公式、前n项和公式,熟练应用公式是解题的关键,同时还考查了学生的运算能力.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
等差数列{an}中有两项am和ak满足am=
,ak=
(其中m,k∈N*,且m≠k),则该数列前mk项之和是( )
| 1 |
| k |
| 1 |
| m |
A、
| ||
B、
| ||
C、
| ||
D、
|