题目内容
首项为3公差为2的等差数列,Sk为其前k项和,则S=![]() +
+![]() +
+![]() +…+
+…+![]() 的值为多少?
的值为多少?
答案:
解析:
提示:
解析:
|
解:Sk=3k+ ∴S= = = = 思路解析:首先根据首项a1=3和公差d=2列出前k项和Sk的表达式,然后根据S= |
提示:
|
形如 |

练习册系列答案
相关题目
 中取出部分项,并将它们按原来的顺序组成一个数列,称之为数列
中取出部分项,并将它们按原来的顺序组成一个数列,称之为数列 、公差为
、公差为
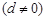 的无穷等差数列.
的无穷等差数列. ,
, 成等比数列,求其公比
成等比数列,求其公比 .
. ,从数列
,从数列 ,从数列
,从数列
 项(设
项(设 )作为一个等比数列的第1项、第2项.求证:当
)作为一个等比数列的第1项、第2项.求证:当 为大于1的正整数时,该数列为
为大于1的正整数时,该数列为 中取出部分项,并将它们按原来的顺序组成一个数列,称之为数列
中取出部分项,并将它们按原来的顺序组成一个数列,称之为数列 、公差为
、公差为
 的无穷等差数列.
的无穷等差数列.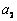 ,
, 成等比数列,求其公比
成等比数列,求其公比 .
. ,从数列
,从数列 ,从数列
,从数列
 项(设
项(设 )作为一个等比数列的第1项、第2项.求证:当
)作为一个等比数列的第1项、第2项.求证:当 为大于1的正整数时,该数列为
为大于1的正整数时,该数列为 中取出部分项,并将它们按原来的顺序组成一个数列,称之为数列
中取出部分项,并将它们按原来的顺序组成一个数列,称之为数列 、公差为
、公差为
 的无穷等差数列.
的无穷等差数列. ,
, 成等比数列,求其公比
成等比数列,求其公比 .
. ,从数列
,从数列 ,从数列
,从数列
 项(设
项(设 )作为一个等比数列的第1项、第2项,试问当且仅当
)作为一个等比数列的第1项、第2项,试问当且仅当 为何值时,该数列为
为何值时,该数列为