题目内容
抛物线y2=4x的焦点弦被焦点分为长为m和n的两部分,则m与n关系为
- A.m+n=4
- B.m•n=4
- C.m+n=m•n
- D.m+n=2m•n
C
分析:假设直线斜率存在,则可设出直线方程与抛物线方程联立消去y可求得x1+x2,再根据抛物线的定义可求得m+n和mn,进而可求得 +
+ =
=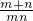 =
=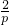 .再看当斜率不存在时,也符合.综合可推断
.再看当斜率不存在时,也符合.综合可推断 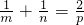 ,然后根据p=2,即可得出结论.
,然后根据p=2,即可得出结论.
解答:抛物线y2=2Px①设AB:y=k(x- ),直线方程与抛物线方程联立消去y得
),直线方程与抛物线方程联立消去y得
得k2x2-(k2p+2p)x+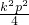 =0.
=0.
∴x1+x2= .
.
又由抛物线定义可得
m+n=x1+x2+p= =
= ,
,
m•n=(x1+ )(x2+
)(x2+ )=
)= ,
,
∴ +
+ =
=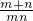 =
=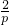 .
.
②若k不存在,则AB方程为x=- ,显然符合本题.
,显然符合本题.
综合①②有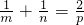
∵p=2
∴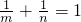 ,即m+n=m•n
,即m+n=m•n
故选C.
点评:本题主要考查了抛物线的简单性质及抛物线与直线的关系.当遇到抛物线焦点弦问题时,常根据焦点设出直线方程与抛物线方程联立,把韦达定理和抛物线定义相结合解决问题.
分析:假设直线斜率存在,则可设出直线方程与抛物线方程联立消去y可求得x1+x2,再根据抛物线的定义可求得m+n和mn,进而可求得
 +
+ =
=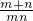 =
=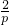 .再看当斜率不存在时,也符合.综合可推断
.再看当斜率不存在时,也符合.综合可推断 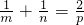 ,然后根据p=2,即可得出结论.
,然后根据p=2,即可得出结论.解答:抛物线y2=2Px①设AB:y=k(x-
 ),直线方程与抛物线方程联立消去y得
),直线方程与抛物线方程联立消去y得得k2x2-(k2p+2p)x+
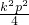 =0.
=0.∴x1+x2=
 .
.又由抛物线定义可得
m+n=x1+x2+p=
 =
= ,
,m•n=(x1+
 )(x2+
)(x2+ )=
)= ,
,∴
 +
+ =
=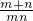 =
=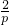 .
.②若k不存在,则AB方程为x=-
 ,显然符合本题.
,显然符合本题.综合①②有
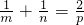
∵p=2
∴
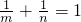 ,即m+n=m•n
,即m+n=m•n故选C.
点评:本题主要考查了抛物线的简单性质及抛物线与直线的关系.当遇到抛物线焦点弦问题时,常根据焦点设出直线方程与抛物线方程联立,把韦达定理和抛物线定义相结合解决问题.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目