Question

（2012•温州二模）函数f（x）=（x+a）（|x-a|+|x-2|）的图象为中心对称图形，则实数a的值为

-

2

3

．

Answer 1

分析：函数f（x）的图象从左到右依次为一段抛物线、一条线段、一段抛物线，对称中心必须是线段的中点．线段中点的横坐标：

a+2

2

，抛物线的对称轴为 x=

-a+  a+2 2

2

，令

a+2

2

=

-a+  a+2 2

2

，解得a的值．

解答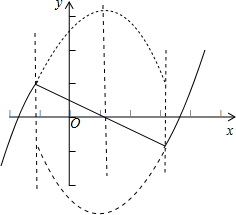：解：∵f（x）=（x+a）（|x-a|+|x-2|），
首先注意到，函数f（x）的图象从左到右依次为一段抛物线、一条线段、一段抛物线．
因此，图形的对称中心必须是线段的中点．（因为直线旋转180°以后只能和自己重合）
另外，两段抛物线要旋转180°以后重合，必须绕着其对称轴上的某个点旋转．
左侧的一段抛物线方程为f（x）=（x+a）（a+2-2x），对称轴为x=

-a+  a+2 2

2

，
中间一条线段的方程为 f（x）=（x+a）|a-x+x-2|=（x+a）•|a-2|，线段中点的横坐标：

a+2

2

，
右侧的一段抛物线方程为f（x）=（x+a）（2x-2-a），对称轴为x=

-a+  a+2 2

2

．
令

a+2

2

=

-a+  a+2 2

2

，解得a=-

2

3

，
故答案为-

2

3

．

点评：本题主要考查绝对值的函数，函数图象的对称性应用，属于中档题．