题目内容
已知点P(x,y)在椭圆x2+2y2=3上运动,则 的最小值是
的最小值是
- A.
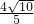
- B.

- C.

- D.2
B
分析:由题意可得x2+2y2=3即x2=3-2y2,则 =
= =
= 利用基本不等式可求最小值
利用基本不等式可求最小值
解答:点P(x,y)在椭圆x2+2y2=3上运动
∴x2+2y2=3即x2=3-2y2
则 =
=
=
=

即所求的最小值为
故选:B
点评:本题主要考查了利用椭圆的方程,利用基本不等式求解最小值,解题的关键是利用了1═ 的代换,从而把所求的式子变形为积为定值的形式
的代换,从而把所求的式子变形为积为定值的形式
分析:由题意可得x2+2y2=3即x2=3-2y2,则
 =
= =
= 利用基本不等式可求最小值
利用基本不等式可求最小值解答:点P(x,y)在椭圆x2+2y2=3上运动
∴x2+2y2=3即x2=3-2y2
则
 =
=
=

=


即所求的最小值为

故选:B
点评:本题主要考查了利用椭圆的方程,利用基本不等式求解最小值,解题的关键是利用了1═
 的代换,从而把所求的式子变形为积为定值的形式
的代换,从而把所求的式子变形为积为定值的形式 
练习册系列答案
相关题目