题目内容
定义在![]() 上的函数
上的函数![]() 同时满足以下条件:
同时满足以下条件:
① ![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数; ②
上是增函数; ② ![]() 是偶函数;
是偶函数;
③ ![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 垂直.
垂直.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)设![]() ,若存在
,若存在![]() ,使
,使![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
解:(Ⅰ)![]() ∵
∵ ![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,
上是增函数,
∴![]() ……① ……………(1分)
……① ……………(1分)
由![]() 是偶函数得:
是偶函数得:![]() ② ……………(2分)
② ……………(2分)
又![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 垂直,
垂直,![]() ③ ……………(3分)
③ ……………(3分)
由①②③得:![]() ,即
,即![]() ……………(4分)
……………(4分)
(Ⅱ)由已知得:若存在![]() ,使
,使![]() ,即存在
,即存在![]() ,使
,使![]() ,
,
设![]() ,则
,则![]() ……………(6分)
……………(6分)
令![]() =0,∵
=0,∵![]() ,∴
,∴![]() ……………(7分)
……………(7分)
当![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 上为减函数
上为减函数
当![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 上为增函数
上为增函数
∴![]() 在
在![]() 上有最大值。……………(9分)
上有最大值。……………(9分)
又![]() ,∴
,∴![]() 最小值为
最小值为![]() ……………(11分)
……………(11分)
于是有![]() 为所求 ……………(12分)
为所求 ……………(12分)

练习册系列答案
相关题目










 上的函数
上的函数 同时满足以下条件:
同时满足以下条件: 在
在 上是减函数,在
上是减函数,在 上是增函数;②
上是增函数;② 是偶函数;
是偶函数; 处的切线与直线
处的切线与直线 垂直.
垂直.  的解析式;
的解析式; ,求函数
,求函数 在
在 上的最小值.
上的最小值. 上的函数
上的函数 同时满足以下条件:
同时满足以下条件: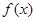 在
在 上是减函数,在
上是减函数,在 上是增函数;②
上是增函数;②  是偶函数;③
是偶函数;③  处的切线与直线
处的切线与直线 垂直.
垂直.  的解析式;
的解析式; ,若存在
,若存在 ,使
,使 ,求实数
,求实数 的取值范围.
的取值范围.