题目内容
定义在
上的函数
同时满足以下条件：
①
在
上是减函数，在
上是增函数；②
是偶函数；
③在
处的切线与直线
垂直.
（Ⅰ）求函数
的解析式；
（Ⅱ）设
，求函数
在
上的最小值.
解：（Ⅰ）
. . …………….…….…………. . …………….…1分
由题意知
即
解得
. …………………4分
所以函数的解析式为
. . …………….…….……5分
（Ⅱ）
， 
.
令
得
，所以函数在
递减，在
递增. . ……7分
当
时，在单调递增，
. . ………9分
当
时，即
时，
在
单调递减，在
单调递增，
. . ……………10分
当
时，即
时，
在单调递减，
. …………….…….12分
综上，在上的最小值
. ………13分
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
上的函数
同时满足：①对任意
，都有
②当
时，
，试解决下列问题： （Ⅰ）求在
时，
的方程
在
上有实数解，求实数
的取值范围；（Ⅲ）若对任意
，关于
都成立，求实数
上的函数
同时满足以下条件：
在
上是减函数，在
上是增函数；②
是偶函数；
处的切线与直线
垂直. 
的解析式；
，求函数
在
上的最小值.
上的函数
同时满足以下条件：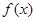
在
上是减函数，在
上是增函数；② 
是偶函数；③ 
处的切线与直线
垂直. 
的解析式；
，若存在
，使
，求实数
的取值范围.