Question

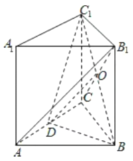
【题目】如图，在三棱柱中，底面，且为正三角形，，为的中点.

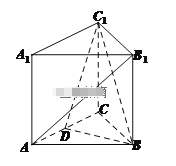
（1）求证：直线平面；

（2）求三棱锥的体积；

（3）三棱柱的顶点都在一个球面上，求该球的体积.

Answer 1

【答案】（1）证明见解析（2）（3）球的体积为

【解析】

（1）连接B1C交BC1于点O，连接OD，可得A1BOD，则直线AB1平面BC1D；

（2）直接利用等积法求三棱锥的体积；

（3）设底面三角形的中心为G，则AG，再设三棱柱的外接球的球心为M，求出半径MA，则球的体积可求.

（1）连接B1C交BC1于点O，连接OD，则O为B1C的中点，

∵D为AC的中点，得DO为的中位线，∴A1BOD，

∵OD平面BC1D，AB1平面BC1D，

∴直线平面；

（2）在正棱柱中，AA1AB6，

∴；

（3）设底面三角形的中心为G，则AG，再设三棱柱的外接球的球心为M，则球的半径为，

∴球的体积为.