题目内容
已知函数![]()
(1)求![]() 的定义域;
的定义域;
(2)在函数![]() 的图象上是否存在不同的两点,使得过这两点的直线平行于x轴;
的图象上是否存在不同的两点,使得过这两点的直线平行于x轴;
(3)当a、b满足什么条件时,![]() 在
在![]() 上恒取正值。
上恒取正值。
(1)![]() 的定义域为
的定义域为![]() 。
。
(2)函数![]() 的图象上不存在不同的两点使过两点的直线平行于x轴。
的图象上不存在不同的两点使过两点的直线平行于x轴。
(3)当![]() 时,
时,![]() 在
在![]() 上恒取正值。
上恒取正值。
解析:
(1)由![]() 得
得![]() ,且
,且![]() ,得
,得![]() ,所以
,所以![]() ,即
,即![]() 的定义域为
的定义域为![]() 。
。
(2)任取![]() ,则
,则![]() ,所以
,所以![]() ,即
,即![]() ,故
,故![]() 。所以
。所以![]() 在
在![]() 为增函数;假设函数
为增函数;假设函数![]() 的图象上存在不同的两点
的图象上存在不同的两点![]() ,使直线平行于x轴,则
,使直线平行于x轴,则![]() 。这与
。这与![]() 是增函数矛盾。故函数
是增函数矛盾。故函数![]() 的图象上不存在不同的两点使过两点的直线平行于x轴。
的图象上不存在不同的两点使过两点的直线平行于x轴。
(3)因为![]() 是增函数,所以当
是增函数,所以当![]() 时,
时,![]() 。这样只需
。这样只需![]() ,即当
,即当![]() 时,
时,![]() 在
在![]() 上恒取正值。
上恒取正值。

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目

 的最小正周期及
的最小正周期及 上的图象.
上的图象. ,
,
 的单调区间;
的单调区间;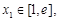 ,都存在
,都存在 ,使得
,使得 ,求
,求 的取值范围。
的取值范围。 知函数
知函数
 的定义域;
的定义域; 上是减函数.
上是减函数. .
. 的最小正周期;
的最小正周期; 上的最大值和最小值以及取得最大值、最小值时x的值.
上的最大值和最小值以及取得最大值、最小值时x的值.