题目内容

如图,在直三棱柱ABC-A1B1C1中,AB=1,![]() ,
,![]()
(1)证明:AB⊥A1C
(2)求二面角A-A1C-B的大小
解:(1)![]() 为直三棱柱,
为直三棱柱,
![]() 底面ABC,
底面ABC,![]()
![]() 三角形ABC中
三角形ABC中 ![]()
由正弦定理得![]() ,
, ![]() …………2分
…………2分
![]() ,
,![]() 平面A1C1CA…………4分
平面A1C1CA…………4分
![]() …………6分
…………6分
(2)连接![]() ,由(1)知正方形A1C1CA对角线
,由(1)知正方形A1C1CA对角线![]() 垂足为H
垂足为H
因为![]() 平面A1C1CA,
平面A1C1CA,![]() AH为BH在平面A1C1CA的内射影
AH为BH在平面A1C1CA的内射影
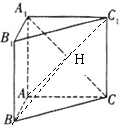 所以
所以![]() 为二面角A—A1C—B的平面角 ……8分
为二面角A—A1C—B的平面角 ……8分
因为在正方形A1C1CA中![]() ,
,
在![]() 中
中![]() ……10分
……10分
 二面角A—A1C—B的大小为arctan
二面角A—A1C—B的大小为arctan![]() ……12分
……12分
解法二:(1)![]() 为直三棱柱,
为直三棱柱,
![]() 底面ABC,
底面ABC,![]()
![]() 三角形ABC中
三角形ABC中 ![]()
由正弦定理得![]() ,
, ![]() …………2分
…………2分
以AB,AC,AA为想,x,y ,z轴建立空间直角坐标系
则A(0, 0, 0),B(1, 0, 0),C(0,![]() ,0),A1(0, 0,
,0),A1(0, 0,![]() )…………4分
)…………4分
![]() ,
,![]() ,
,![]()
![]()
![]()
![]() …………6分
…………6分
(2)设平面A1BC的法向量为![]()
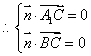 即
即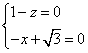 得
得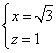
![]() …………10分
…………10分
因为平面ACC1A1的法向量为![]()
![]()
即二面角A—A1C—B的大小为![]() …………12分
…………12分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目




