题目内容
在△ABC中,内角A,B,C的对边分别为a,b,c,已知a,b,c成等比数列,且cosB= .
.
(1)若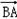 ·
·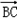 =
= ,求a+c的值;
,求a+c的值;
(2)求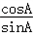 +
+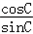 的值.
的值.
 .
.(1)若
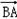 ·
·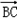 =
= ,求a+c的值;
,求a+c的值;(2)求
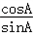 +
+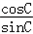 的值.
的值.解:(1)由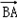 ·
·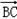 =
= 可得 accosB=
可得 accosB= ,
,
因为 cosB= ,所以b2=ac=2.
,所以b2=ac=2.
由余弦定理b2=a2+c2﹣2accosB,
得a2+c2=b2+2accosB=5,
则(a+c)2=a2+c2+2ac=9,
故a+c=3.
(2)由cosB= 可得 sinB=
可得 sinB=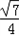 .
.
由b2=ac及正弦定理得sin2B=sinAsinC,
于是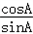 +
+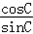 =
=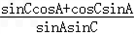
=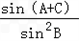 =
=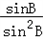 =
=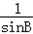 =
=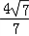 .
.
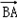 ·
·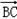 =
= 可得 accosB=
可得 accosB= ,
,因为 cosB=
 ,所以b2=ac=2.
,所以b2=ac=2.由余弦定理b2=a2+c2﹣2accosB,
得a2+c2=b2+2accosB=5,
则(a+c)2=a2+c2+2ac=9,
故a+c=3.
(2)由cosB=
 可得 sinB=
可得 sinB=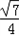 .
.由b2=ac及正弦定理得sin2B=sinAsinC,
于是
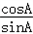 +
+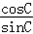 =
=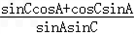
=
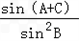 =
=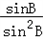 =
=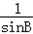 =
=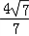 .
.
练习册系列答案
相关题目