题目内容
给出下列命题:①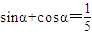 ,则α在第一或四象限;②函数y=sinx+cosx,
,则α在第一或四象限;②函数y=sinx+cosx,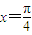 是它的一条对称轴,
是它的一条对称轴, 是它的一个对称中心;③函数
是它的一个对称中心;③函数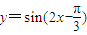 在
在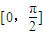 内是单调增函数;④把
内是单调增函数;④把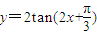 的图象向右平移
的图象向右平移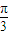 个单位可得到y=2tan2x的图象;⑤在△ABC中,cos2A>cos2B是A<B的充要条件.
个单位可得到y=2tan2x的图象;⑤在△ABC中,cos2A>cos2B是A<B的充要条件.其中逆否命题为真命题的有( )
A.①②⑤
B.②⑤
C.②③④
D.①③⑤
【答案】分析:将①中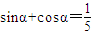 两边平方后,我们易求出sinα•cosα,由其符号可判断α所在的象限;将
两边平方后,我们易求出sinα•cosα,由其符号可判断α所在的象限;将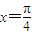 ,
,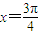 分别代入函数y=sinx+cosx,根据其值是否为函数的最值,易判断
分别代入函数y=sinx+cosx,根据其值是否为函数的最值,易判断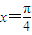 是否是它的一条对称轴,根据其值是否为0,可判断
是否是它的一条对称轴,根据其值是否为0,可判断 是否是它的一个对称中心;利用三角函数的单调性,可判断③的真假;根据函数平移变换法则,可判断④的对错;由倍角公式及正弦定理,我们也可得到⑤的正误.进行得到结论.
是否是它的一个对称中心;利用三角函数的单调性,可判断③的真假;根据函数平移变换法则,可判断④的对错;由倍角公式及正弦定理,我们也可得到⑤的正误.进行得到结论.
解答:解:对于①, ⇒
⇒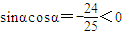 ,∴α在第二或四象限,错误.
,∴α在第二或四象限,错误.
对于②,y=sinx+cosx= ,
, 时,
时,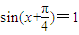 ,∴
,∴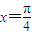 是它的一条对称轴,
是它的一条对称轴,
 时,
时,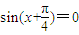 ,∴
,∴ 是它的一个对称中心,正确.
是它的一个对称中心,正确.
对于③,在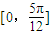 内
内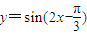 单增,在
单增,在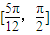 单减,∴错误.
单减,∴错误.
对于④,把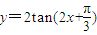 的图象向右平移
的图象向右平移 个单位得到
个单位得到 ≠2tan2x,∴错误.
≠2tan2x,∴错误.
对于⑤,在△ABC中,cos2A>cos2B?1-2sin2A>1-2sin2B?sinA<sinB?a<b?A<B,∴正确
故选:B
点评:本题考查的知识点是三角函数的定义,符号,对称性,单调性,平移变换,倍角公式,正弦定理及命题真假的判断,熟练掌握三角函数的定义和性质,是解答本题的关键.
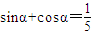 两边平方后,我们易求出sinα•cosα,由其符号可判断α所在的象限;将
两边平方后,我们易求出sinα•cosα,由其符号可判断α所在的象限;将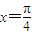 ,
,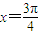 分别代入函数y=sinx+cosx,根据其值是否为函数的最值,易判断
分别代入函数y=sinx+cosx,根据其值是否为函数的最值,易判断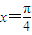 是否是它的一条对称轴,根据其值是否为0,可判断
是否是它的一条对称轴,根据其值是否为0,可判断 是否是它的一个对称中心;利用三角函数的单调性,可判断③的真假;根据函数平移变换法则,可判断④的对错;由倍角公式及正弦定理,我们也可得到⑤的正误.进行得到结论.
是否是它的一个对称中心;利用三角函数的单调性,可判断③的真假;根据函数平移变换法则,可判断④的对错;由倍角公式及正弦定理,我们也可得到⑤的正误.进行得到结论.解答:解:对于①,
 ⇒
⇒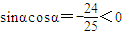 ,∴α在第二或四象限,错误.
,∴α在第二或四象限,错误.对于②,y=sinx+cosx=
 ,
, 时,
时,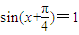 ,∴
,∴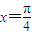 是它的一条对称轴,
是它的一条对称轴, 时,
时,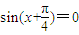 ,∴
,∴ 是它的一个对称中心,正确.
是它的一个对称中心,正确.对于③,在
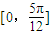 内
内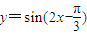 单增,在
单增,在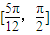 单减,∴错误.
单减,∴错误.对于④,把
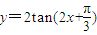 的图象向右平移
的图象向右平移 个单位得到
个单位得到 ≠2tan2x,∴错误.
≠2tan2x,∴错误.对于⑤,在△ABC中,cos2A>cos2B?1-2sin2A>1-2sin2B?sinA<sinB?a<b?A<B,∴正确
故选:B
点评:本题考查的知识点是三角函数的定义,符号,对称性,单调性,平移变换,倍角公式,正弦定理及命题真假的判断,熟练掌握三角函数的定义和性质,是解答本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目