题目内容
设函数![]()
(1)求函数![]() 的单调区间;
的单调区间;
(2)若![]() ,求不等式
,求不等式![]() 的解集.
的解集.
解: (1) ![]() ,
,
由![]() ,得
,得 ![]() .
.
因为 当![]() 时,
时,![]() ; 当
; 当![]() 时,
时,![]() ; 当
; 当![]() 时,
时,![]() ;
;
所以![]() 的单调增区间是:
的单调增区间是:![]() ; 单调减区间是:
; 单调减区间是: ![]() .…………6分
.…………6分
(2) 由 ![]()
![]() ,
,
得:![]() .
.
故:当 ![]() 时, 解集是:
时, 解集是:![]() ;
;
当 ![]() 时,解集是:
时,解集是: ![]() ;
;
当![]() 时, 解集是:
时, 解集是:![]() . 网 …………13分
. 网 …………13分

练习册系列答案
相关题目
 设函数
设函数 (2009•成都模拟)设函数
(2009•成都模拟)设函数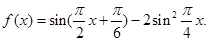
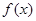 的最小正周期;
的最小正周期;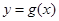 的图像与函数
的图像与函数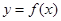 的图像关于原点对称,求
的图像关于原点对称,求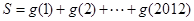 的值。
的值。