题目内容
(本题满分14分)如图,在四棱锥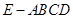 中,四边形
中,四边形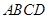 为平行四边形,
为平行四边形,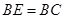 ,
,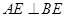 ,
,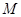 为
为 上一点,且
上一点,且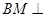 平面
平面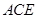 .
.
⑴求证: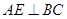 ;
;
⑵如果点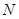 为线段
为线段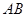 的中点,求证:
的中点,求证: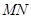 ∥平面
∥平面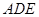 .
.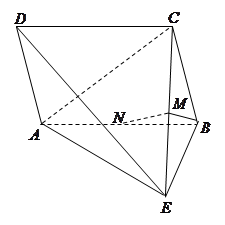
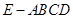 中,四边形
中,四边形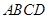 为平行四边形,
为平行四边形,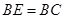 ,
,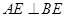 ,
,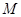 为
为 上一点,且
上一点,且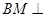 平面
平面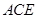 .
.⑴求证:
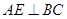 ;
;⑵如果点
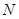 为线段
为线段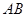 的中点,求证:
的中点,求证: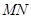 ∥平面
∥平面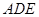 .
.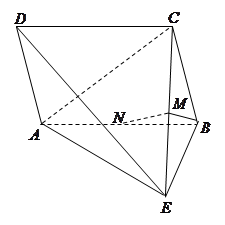
见解析.
(1)本小题可以通过证明 平面
平面 ,来证明
,来证明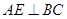 .
.
(2) 取 中点
中点 ,通过证明四边形
,通过证明四边形 为平行四边形,从而证明出
为平行四边形,从而证明出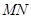 ∥
∥ ,问题得解。
,问题得解。
证明:⑴因为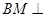 平面
平面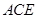 ,
, 平面
平面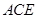 ,所以
,所以 .…2分
.…2分
因为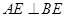 ,且
,且 ,
, 平面
平面 ,
,
所以 平面
平面 .……………………………………………………………………4分
.……………………………………………………………………4分
因为 平面
平面 ,所以
,所以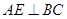 .………………………………………………6分
.………………………………………………6分
⑵取 中点
中点 ,连结
,连结 .
.
因为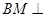 平面
平面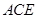 ,
, 平面
平面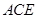 ,所以
,所以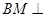
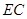 .
.
因为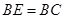 ,所以
,所以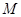 为
为 的中点.………………………………………………8分
的中点.………………………………………………8分
所以 为△
为△ 的中位线.所以
的中位线.所以 ∥
∥ ,且
,且 =
= .……………10分
.……………10分
因为四边形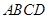 为平行四边形,所以
为平行四边形,所以 ∥
∥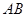 ,且
,且

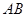 .
.
故 ∥
∥ ,且
,且

 .
.
因为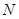 为
为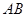 中点,所以
中点,所以 ∥
∥ ,且
,且

 .
.
所以四边形 为平行四边形,所以
为平行四边形,所以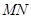 ∥
∥ .………………………………12分
.………………………………12分
因为 平面
平面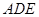 ,
, 平面
平面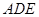 ,所以
,所以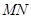 ∥平面
∥平面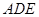 .………………14分
.………………14分
 平面
平面 ,来证明
,来证明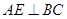 .
.(2) 取
 中点
中点 ,通过证明四边形
,通过证明四边形 为平行四边形,从而证明出
为平行四边形,从而证明出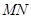 ∥
∥ ,问题得解。
,问题得解。证明:⑴因为
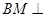 平面
平面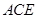 ,
, 平面
平面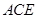 ,所以
,所以 .…2分
.…2分因为
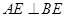 ,且
,且 ,
, 平面
平面 ,
,所以
 平面
平面 .……………………………………………………………………4分
.……………………………………………………………………4分因为
 平面
平面 ,所以
,所以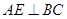 .………………………………………………6分
.………………………………………………6分⑵取
 中点
中点 ,连结
,连结 .
.因为
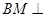 平面
平面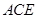 ,
, 平面
平面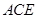 ,所以
,所以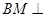
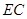 .
.因为
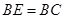 ,所以
,所以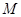 为
为 的中点.………………………………………………8分
的中点.………………………………………………8分所以
 为△
为△ 的中位线.所以
的中位线.所以 ∥
∥ ,且
,且 =
= .……………10分
.……………10分因为四边形
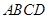 为平行四边形,所以
为平行四边形,所以 ∥
∥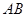 ,且
,且

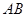 .
.故
 ∥
∥ ,且
,且

 .
.因为
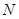 为
为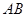 中点,所以
中点,所以 ∥
∥ ,且
,且

 .
.所以四边形
 为平行四边形,所以
为平行四边形,所以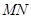 ∥
∥ .………………………………12分
.………………………………12分因为
 平面
平面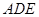 ,
, 平面
平面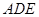 ,所以
,所以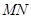 ∥平面
∥平面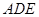 .………………14分
.………………14分
练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
 的底面是直角三角形,
的底面是直角三角形, ,点
,点 在底面内的射影恰好是
在底面内的射影恰好是 的中点,且
的中点,且 .
.

 平面
平面 ;
; 的余弦值为
的余弦值为 ,设
,设 ,求
,求 的值.
的值. 中,E是棱
中,E是棱 的中点,则BE与平面
的中点,则BE与平面 所成角的正弦值为
所成角的正弦值为



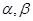 为两个不同的平面,下列四个命题中,正确的命题个数是
为两个不同的平面,下列四个命题中,正确的命题个数是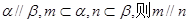 ;
;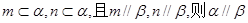
 ;
; 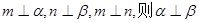
 是两个不重合的平面,
是两个不重合的平面, 是两条不同的直线,给出下列命题:
是两条不同的直线,给出下列命题: ∥
∥ ,
, ∥
∥ ∥
∥ ∥
∥ ,则
,则 ∥
∥ 则
则
 ∥
∥ ∥
∥ ,其中正确的有 (只填序号)
,其中正确的有 (只填序号) 面ABCD,E是PD的中点。
面ABCD,E是PD的中点。
 平面PDA;
平面PDA;

 ,
, 是两个不同的平面, m,n是两条不重合的直线,下列命题中正确的是
是两个不同的平面, m,n是两条不重合的直线,下列命题中正确的是