题目内容
如图,已知正方形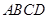 的边长为1,
的边长为1,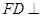 平面
平面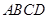 ,
,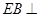 平面
平面 ,
,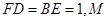 为
为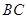 边上的动点。
边上的动点。
(1)证明: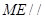 平面
平面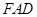 ;
;
(2)试探究点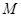 的位置,使平面
的位置,使平面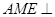 平面
平面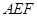 。
。
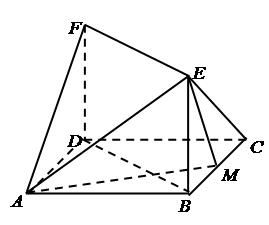
 的边长为1,
的边长为1,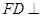 平面
平面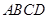 ,
,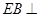 平面
平面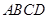 ,
,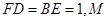 为
为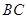 边上的动点。
边上的动点。(1)证明:
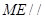 平面
平面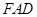 ;
; (2)试探究点
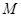 的位置,使平面
的位置,使平面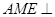 平面
平面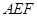 。
。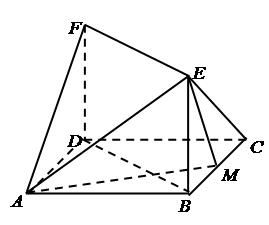
解:(1)∵ FD⊥平面ABCD,EB⊥平面ABCD
∴FD∥EB
又AD∥BC且AD∩FD=D,BC∩BE=B
∴平面FAD∥平面EBC,ME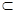 平面EBC
平面EBC
∴ME∥平面FAD ……………………4分
(2)以D为坐标原点,分别以DA、DC、DF所在直线为x、y、z轴,建立空间直角坐标D-xyz,
依题意,得D(0,0,0),A(1,0,0),F(0,0,1),C(0,1,0),B(1,1,0),E(1,1,1),
设M(λ,1,0),平面AEF的法向量为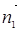 =(x1,y1,z1),平面AME的法向量为
=(x1,y1,z1),平面AME的法向量为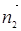 =(x2,y2,z2)
=(x2,y2,z2)
∵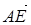 =(0,1,1),
=(0,1,1),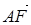 =(-1,0,1), ∴
=(-1,0,1), ∴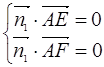 ∴
∴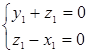
取z1=1,得x1=1,y1=-1 ∴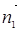 =(1,-1,0)
=(1,-1,0)
又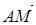 =(λ-1,1,0) ,
=(λ-1,1,0) ,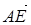 =(0,1,1),
=(0,1,1),
∴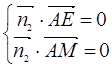 ∴
∴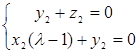
取x2=1得y2=1-λ,z2=λ-1 ∴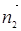 =(1,1-λ,λ-1)
=(1,1-λ,λ-1)
若平面AME⊥平面AEF,则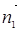 ⊥
⊥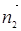 ∴
∴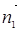
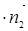 =0,
=0,
∴1-(1-λ)+(λ-1)=0,解得λ=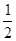 ,
,
此时M为BC的中点.
所以当M在BC的中点时, AME⊥平面AEF. ……………12分
∴FD∥EB
又AD∥BC且AD∩FD=D,BC∩BE=B
∴平面FAD∥平面EBC,ME
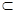 平面EBC
平面EBC∴ME∥平面FAD ……………………4分
(2)以D为坐标原点,分别以DA、DC、DF所在直线为x、y、z轴,建立空间直角坐标D-xyz,
依题意,得D(0,0,0),A(1,0,0),F(0,0,1),C(0,1,0),B(1,1,0),E(1,1,1),
设M(λ,1,0),平面AEF的法向量为
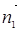 =(x1,y1,z1),平面AME的法向量为
=(x1,y1,z1),平面AME的法向量为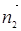 =(x2,y2,z2)
=(x2,y2,z2)∵
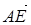 =(0,1,1),
=(0,1,1),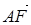 =(-1,0,1), ∴
=(-1,0,1), ∴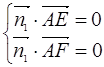 ∴
∴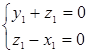
取z1=1,得x1=1,y1=-1 ∴
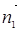 =(1,-1,0)
=(1,-1,0) 又
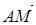 =(λ-1,1,0) ,
=(λ-1,1,0) ,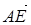 =(0,1,1),
=(0,1,1),∴
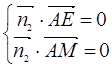 ∴
∴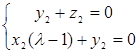
取x2=1得y2=1-λ,z2=λ-1 ∴
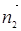 =(1,1-λ,λ-1)
=(1,1-λ,λ-1)若平面AME⊥平面AEF,则
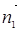 ⊥
⊥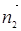 ∴
∴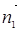
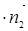 =0,
=0,∴1-(1-λ)+(λ-1)=0,解得λ=
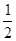 ,
,此时M为BC的中点.
所以当M在BC的中点时, AME⊥平面AEF. ……………12分
略

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
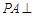 矩形
矩形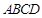 所在平面,
所在平面,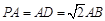 ,
,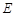 为线段
为线段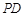 上一点,
上一点,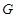 为线段
为线段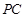
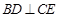 ;
;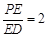 时,求证:BG//平面AEC.
时,求证:BG//平面AEC.
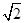 ,E为PD上一点,PE = 2ED.
,E为PD上一点,PE = 2ED.
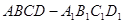 中,点
中,点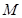 为线段
为线段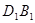 上的动点,点
上的动点,点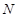 为线段
为线段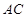 上的动点,则与线段
上的动点,则与线段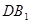 相交且互相平分的线段
相交且互相平分的线段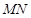 有( )
有( )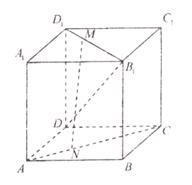
 中(图1),
中(图1), 是
是 的中点,
的中点, ,
,
 ,
, 将(图1)沿直线
将(图1)沿直线 折起,使二面角
折起,使二面角 为
为 (如图2)
(如图2) 平面
平面 ;
; 与
与 所成角的余弦值;
所成角的余弦值; 到平面
到平面 的距离.
的距离.


 -
- 中,异面直线
中,异面直线 与
与 所成角的大小为 ▲ ;
所成角的大小为 ▲ ; 中,
中, 是
是 的中点。
的中点。 上求一点
上求一点 ,使
,使 平面
平面 ;
; 的余弦值.
的余弦值.