题目内容
11.已知f(x)=tanx,则${f^'}(\frac{4π}{3})$等于$\sqrt{3}$.分析 根据f(x)=tanx,求得f($\frac{4π}{3}$)的值.
解答 解:由f(x)=tanx,可得${f^'}(\frac{4π}{3})$=tan$\frac{4π}{3}$=tan$\frac{π}{3}$=$\sqrt{3}$,
故答案为:$\sqrt{3}$.
点评 本题主要考查求正切函数的值,属于基础题.

练习册系列答案
相关题目
2.三棱柱ABC-A1B1C1中,侧棱AA1丄底面A1B1C1,底面三角形是正三角形,E是BC中点,则下列叙述正确的是( )
| A. | CC1与B1E是异面直线 | B. | AC丄平面ABB1A1 | ||
| C. | AE 丄 B1C1 | D. | A1C1∥平面AB1E |
3.设函数f(x)=$\frac{1}{x}$-$\frac{m}{{x}^{2}}$-$\frac{x}{3}$,若?x∈(0,+∞),f(x)<0恒成立,则实数m的取值范围为( )
| A. | ($\frac{2}{3}$,1) | B. | ($\frac{2}{3}$,2) | C. | ($\frac{2}{3}$,+∞) | D. | (-∞,$\frac{2}{3}$) |
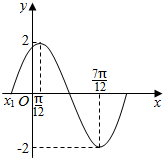 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)在一个周期内的图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)在一个周期内的图象如图所示.