题目内容
【题目】已知数列![]() 满足:
满足:![]() .
.
(1)写出数列的前6项的值;
(2)猜想数列![]() 与
与![]() 的单调性,选择一种情形证明你的结论.
的单调性,选择一种情形证明你的结论.
【答案】(1)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)由已知得![]() ,由此依次求得
,由此依次求得![]() ;
;
(2)由归纳法得出数列![]() 与
与![]() 的单调性,并用数学归纳法证明.
的单调性,并用数学归纳法证明.
(1)∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
(2)由(1) 结论:![]() 是递增数列,
是递增数列,![]() 是递减数列.
是递减数列.
由![]() ,得
,得![]() ,由
,由![]() 知数列
知数列![]() 是正项数列,
是正项数列,
①证![]() 是递增数列,即证
是递增数列,即证![]() 对一切正整数
对一切正整数![]() 恒成立,
恒成立,
(i)显然![]() ,即
,即![]() 时,不等式成立,
时,不等式成立,
(ii)假设![]() 时,不等式成立,即
时,不等式成立,即![]() ,∴
,∴![]() ,则
,则![]() ,
,![]() ,即
,即![]() ,
,
易知函数![]() 在
在![]() 上是增函数,
上是增函数,
∴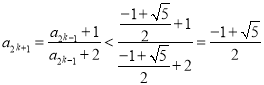 ,
,
∴![]()
![]()
![]()
 ,
,
∵![]() ,∴
,∴![]() ,即
,即![]() ,
,
∴![]() 时,不等式成立,
时,不等式成立,
综合(i)(ii)可知对一切正整数![]() ,
,![]() 成立,即
成立,即![]() 是递增数列.
是递增数列.
②证![]() 是递减数列,即证
是递减数列,即证![]() 对一切正整数
对一切正整数![]() 恒成立,
恒成立,
(i)显然![]() ,即
,即![]() 时,不等式成立,
时,不等式成立,
(ii)假设![]() 时,不等式成立,即
时,不等式成立,即![]() ,∴
,∴![]() ,则
,则![]() ,
,![]() ,(
,(![]() 舍去),
舍去),
易知函数![]() 在
在![]() 上是增函数,
上是增函数,
∴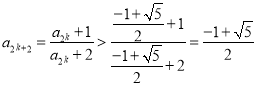 ,
,
∴![]()
![]()
![]()
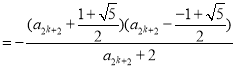 ,
,
∵![]() ,∴
,∴![]() ,即
,即![]() ,
,
∴![]() 时,不等式成立,
时,不等式成立,
综合(i)(ii)可知对一切正整数![]() ,
,![]() 成立,即
成立,即![]() 是递减数列.
是递减数列.

练习册系列答案
相关题目