题目内容
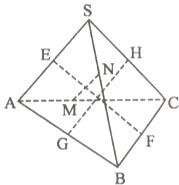如图，在四面体S-ABC中，E、F、G、H、M、N分别是棱SA、BC、AB、SC、AC、SB的中点，且EF=GH=MN，求证：SA⊥BC，SB⊥AC，SC⊥AB．
分析：本题是一个证明线线垂直的问题，可以取SA，SB，SC三个有向线段对应的向量为基向量，将SA，BC，SB，AC，SC，AB这六个线段对应的向量用基向量表示出来利用数量积为0证明线线垂直．
解答：证明：如图，设
=
，
=
，
=
，则
，
，
，
，
，
分别为
，
(
+
)，
(
+
)，
，
(
+
)，
…（4分）
由条件EF=GH=MN得：(
)2=(
)2=(
)2
展开得
•
=
•
=
•
…（7分）
∴
(
-
)=0∵
≠
，
-
≠
…（9分）
∴
⊥(
-
)，即SA⊥BC…（12分）
同理可证SB⊥AC，SC⊥AB…（14分）
| SA |
| r1 |
| SB |
| r2 |
| SC |
| r3 |
| SE |
| SF |
| SG |
| SH |
| SM |
| SN |
分别为
| 1 |
| 2 |
| r1 |
| 1 |
| 2 |
| r2 |
| r3 |
| 1 |
| 2 |
| r1 |
| r2 |
| 1 |
| 2 |
| r3 |
| 1 |
| 2 |
| r1 |
| r3 |
| 1 |
| 2 |
| r2 |
由条件EF=GH=MN得：(
-
| ||||||
| 2 |
| ||||||
| 2 |
| ||||||
| 2 |
展开得
| r1 |
| r2 |
| r2 |
| r3 |
| r1 |
| r3 |
∴
| r1• |
| r2 |
| r3 |
| r1 |
| 0 |
| r2 |
| r3 |
| 0 |
∴
| r1 |
| r2 |
| r3 |
同理可证SB⊥AC，SC⊥AB…（14分）
点评：本题考查用向量语言表述线线的垂直关系，解题的关键是将垂直证明问题转化为向量运算，利用向量的数量积为0证明线线垂直，利用空间向量证明几何问题是向量的重要运用，在近几年的高考中，这是一个比较热的考点
练习册系列答案
黎明文化寒假作业系列答案
相关题目
如图，在棱长相等的四面体S-ABC中，E、F分别是SC、AB的中点，则直线EF与SA所成的角为（ ）| A、90° | B、60° | C、45° | D、30° |
