题目内容
17.已知在△ABC中,角A、B、C的对边分别是a、b、c,且2sin2A+3cos(B+C)=0.(1)求角A的大小;
(2)若△ABC的面积S=$5\sqrt{3},c=4$,求sinB+sinC的值.
分析 (1)由题意可得cosA的方程,解得cosA=$\frac{1}{2}$,A=$\frac{π}{3}$;
(2)由三角形的面积公式可得b和c的值,由余弦定理可得a,整体代入sinB+sinC=$\frac{sinA}{a}$×(b+c),计算可得.
解答 解:(1)∵在△ABC中2sin2A+3cos(B+C)=0,
∴2(1-cos2A)-3cosA=0,解得cosA=$\frac{1}{2}$,或cosA=-2(舍去),
∵0<A<π,∴角A=$\frac{π}{3}$;
(2)∵△ABC的面积S=$\frac{1}{2}$bcsinA=$\frac{\sqrt{3}}{4}$bc=5$\sqrt{3}$,∴bc=20,
再由c=4可得b=5,故b+c=9,由余弦定理可得:
a2=b2+c2-2bccosA=(b+c)2-3bc=21,∴a=$\sqrt{21}$,
∴sinB+sinC=$\frac{bsinA}{a}$+$\frac{csinA}{a}$=$\frac{sinA}{a}$×(b+c)=$\frac{\sqrt{3}}{2×\sqrt{21}}$×9=$\frac{9\sqrt{7}}{14}$
点评 本题考查正余弦定理解三角形,涉及三角形的面积公式和整体代入的思想,属中档题.

练习册系列答案
相关题目
2.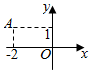 如图,在复平面内,表示复数z的点为A,则复数$\frac{z}{1-2i}$对应的点在( )
如图,在复平面内,表示复数z的点为A,则复数$\frac{z}{1-2i}$对应的点在( )
 如图,在复平面内,表示复数z的点为A,则复数$\frac{z}{1-2i}$对应的点在( )
如图,在复平面内,表示复数z的点为A,则复数$\frac{z}{1-2i}$对应的点在( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
9.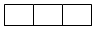 用2种不同颜色给图中3个矩形随机涂色,每个矩形只涂一种颜色,则3个矩形中相邻矩形颜色不同的概率是( )
用2种不同颜色给图中3个矩形随机涂色,每个矩形只涂一种颜色,则3个矩形中相邻矩形颜色不同的概率是( )
 用2种不同颜色给图中3个矩形随机涂色,每个矩形只涂一种颜色,则3个矩形中相邻矩形颜色不同的概率是( )
用2种不同颜色给图中3个矩形随机涂色,每个矩形只涂一种颜色,则3个矩形中相邻矩形颜色不同的概率是( )| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{2}$ |
6.(1+x)4的展开式中x2的系数为( )
| A. | 1 | B. | 4 | C. | 6 | D. | 12 |
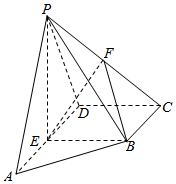 在四棱锥P-ABCD中,平面PAD⊥平面ABCD,四边形ABCD为直角梯形,BC∥AD,∠ADC=90°,BC=CD=$\frac{1}{2}$AD=1,PA=PD,E,F分别为线段AD,PC的中点.
在四棱锥P-ABCD中,平面PAD⊥平面ABCD,四边形ABCD为直角梯形,BC∥AD,∠ADC=90°,BC=CD=$\frac{1}{2}$AD=1,PA=PD,E,F分别为线段AD,PC的中点.