题目内容
设a=∫0π(sinx+cosx)dx,则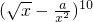 展开式中的常数项是________.
展开式中的常数项是________.
180
分析:直接求出定积分的值,求出a的值,然后根据二项式展开的公式将二项式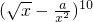 展开,令x的幂指数为0,求出r,从而求解.
展开,令x的幂指数为0,求出r,从而求解.
解答:∵a=∫0π(sinx+cosx)dx=(-cosx+sinx)|0π=(-cosπ+sinπ)-(-cos0+sin0)=2,
所以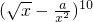 =
= ,它的通项公式为:Tr+1=(-1)rC10r(
,它的通项公式为:Tr+1=(-1)rC10r(  )10-r(
)10-r(  )r=(-1)rC10r2r
)r=(-1)rC10r2r
令10-5r=0,得r=2,因此,展开式中常数项是:(-1)2C10222=180.
故答案为:180.
点评:本题考查了简单定积分的计算以及求二项式展开式的指定项的基本方法.考查计算能力,基本功.
分析:直接求出定积分的值,求出a的值,然后根据二项式展开的公式将二项式
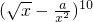 展开,令x的幂指数为0,求出r,从而求解.
展开,令x的幂指数为0,求出r,从而求解.解答:∵a=∫0π(sinx+cosx)dx=(-cosx+sinx)|0π=(-cosπ+sinπ)-(-cos0+sin0)=2,
所以
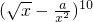 =
= ,它的通项公式为:Tr+1=(-1)rC10r(
,它的通项公式为:Tr+1=(-1)rC10r(  )10-r(
)10-r(  )r=(-1)rC10r2r
)r=(-1)rC10r2r
令10-5r=0,得r=2,因此,展开式中常数项是:(-1)2C10222=180.
故答案为:180.
点评:本题考查了简单定积分的计算以及求二项式展开式的指定项的基本方法.考查计算能力,基本功.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目