题目内容
在三棱柱ABC-A1B1C1中,底面是正三角形,侧棱AA1⊥底面ABC,且各棱长都相等点E是边AB的中点,则直线C1E与平面BB1CC1所成角的正切值为( )
分析:过点E作EF⊥BC于点F,连接FC1,可证明∠EC1F即为直线C1E与平面BB1CC1所成角,设各棱长为1,通过解直角三角形可求得EF,FC1的长,从而可求tan∠EC1F=
.
| EF |
| FC1 |
解答: 解:如下图所示:过点E作EF⊥BC于点F,连接FC1,
解:如下图所示:过点E作EF⊥BC于点F,连接FC1,
因为BB1∥AA1,AA1⊥底面ABC,所以BB1⊥底面ABC,
BB1?面BC1,所以面BB1⊥底面ABC,
所以EF⊥面BC1,则∠EC1F即为直线C1E与平面BB1CC1所成角,
设各棱长为1,在Rt△EFB中,EF=BE•sin∠EBF=
×sin60°=
,BF=BE•cos∠EBF=
×cos60°=
,
在Rt△C1CF中,C1F=
=
=
,
所以tan∠EC1F=
=
=
.
故选A.
 解:如下图所示:过点E作EF⊥BC于点F,连接FC1,
解:如下图所示:过点E作EF⊥BC于点F,连接FC1,因为BB1∥AA1,AA1⊥底面ABC,所以BB1⊥底面ABC,
BB1?面BC1,所以面BB1⊥底面ABC,
所以EF⊥面BC1,则∠EC1F即为直线C1E与平面BB1CC1所成角,
设各棱长为1,在Rt△EFB中,EF=BE•sin∠EBF=
| 1 |
| 2 |
| ||
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
在Rt△C1CF中,C1F=
| C1C2+CF2 |
12+(
|
| 5 |
| 4 |
所以tan∠EC1F=
| EF |
| FC1 |
| ||||
|
| ||
| 5 |
故选A.
点评:本题考查直线与平面所成的角的求解问题,考查学生的计算能力,属中档题,准确理解线面角的定义是解决该类题目的基础.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
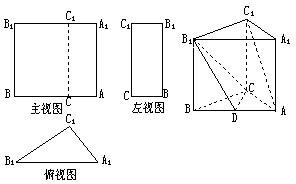 已知三棱柱ABC-A1B1C1的三视图如图所示,其中主视图AA1B1B和左视图B1BCC1均为矩形,在俯视图△A1B1C1中,A1C1=3,A1B1=5,
已知三棱柱ABC-A1B1C1的三视图如图所示,其中主视图AA1B1B和左视图B1BCC1均为矩形,在俯视图△A1B1C1中,A1C1=3,A1B1=5, 如图:在正三棱柱ABC-A1 B1 C1中,AB=
如图:在正三棱柱ABC-A1 B1 C1中,AB= 在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=
在三棱柱ABC-A1B1C1中,已知AB=AC=AA1= (2012•江西)在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=
(2012•江西)在三棱柱ABC-A1B1C1中,已知AB=AC=AA1= (2013•北京)如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.
(2013•北京)如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.