题目内容
(本小题满分12分)已知函数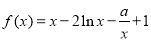 ,
,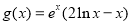 .
.
(Ⅰ)若函数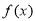 在定义域上是增函数,求a的取值范围;
在定义域上是增函数,求a的取值范围;
(Ⅱ)求 的最大值.
的最大值.
(1)[1,+∞);(2)-e.
【解析】
试题分析:本题主要考查导数的运算、利用导数判断函数的单调性、利用导数求函数的最值和极值等基础知识,意在考查考生的分析问题解决问题的能力、转化能力、运算求解能力.第一问,先对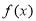 求导,将函数
求导,将函数 在定义域上是增函数,转化为
在定义域上是增函数,转化为 恒成立,即转化为
恒成立,即转化为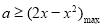 ,配方法得到
,配方法得到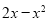 的最大值,即可得到a的取值范围;第二问,先对
的最大值,即可得到a的取值范围;第二问,先对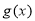 求导,结合第一问的结论,知
求导,结合第一问的结论,知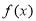 在定义域上是增函数,且
在定义域上是增函数,且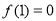 ,利用
,利用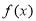 的单调性,得到
的单调性,得到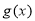 的单调性,从而知当
的单调性,从而知当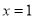 时
时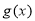 取得最大值.
取得最大值.
试题解析:(Ⅰ)由题意得x>0,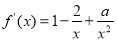 . 1分
. 1分
由函数f(x)在定义域上是增函数得,f(x)≥0,即a≥2x-x2=-(x-1)2+1(x>0).
因为-(x-1)2+1≤1(当x=1时,取等号),
所以a的取值范围是[1,+∞). 5分
(Ⅱ)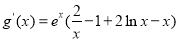 , 7分
, 7分
由(Ⅰ)得a=2时,f(x)=x-2lnx-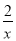 +1
+1
且f(x)在定义域上是增函数得,又f(1)=0,
所以,当x∈(0,1)时,f(x)<0,当x∈(1,+∞)时,f(x)>0. 10分
所以,当x∈(0,1)时,g(x)>0,当x∈(1,+∞)时,g(x)<0.
故x=1时,g(x)取得最大值-e. 12分
考点:导数的运算、利用导数判断函数的单调性、利用导数求函数的最值和极值.
考点分析: 考点1:导数及其应用 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
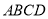 中,
中, ,
,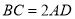 ,
,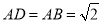 ,
,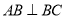 ,如图把
,如图把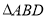 沿
沿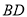 翻折,使得平面
翻折,使得平面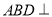 平面
平面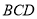 .
.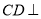 平面
平面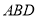 ;
;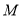 为线段
为线段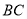 中点,求点
中点,求点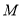 到平面
到平面 的距离.
的距离.
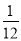 B.
B.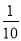 C.
C.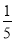 D.
D.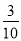
 ,表示的平面区域为M,若直线
,表示的平面区域为M,若直线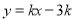 与平面区域M有公共点,则k的取值范围是( )
与平面区域M有公共点,则k的取值范围是( )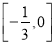 B.
B. 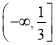 C.
C. 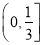 D.
D. 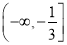
 满足
满足 ,则
,则 B.
B.  C.
C.  D.
D. 
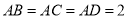 ,则平面BCD被球所截面图形的面积为 .
,则平面BCD被球所截面图形的面积为 . ,则
,则 ( )
( ) B.
B. C.
C. 或0
或0 ,满足
,满足 ,则
,则 的取值范围为 .
的取值范围为 . 在角
在角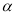 的终边上,点
的终边上,点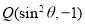 在角
在角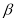 的终边上,且
的终边上,且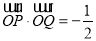 .
.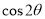 的值;(2)求
的值;(2)求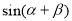 的值.
的值.